ICML2020的论文《Do We Need Zero Training Loss After Achieving Zero Training Error?》提出了一种Flooding方法,用于缓解模型过拟合,详情可以看我的文章《我们真的需要把训练集的损失降到零吗?》。这里简单过一下,论文提出了一个超参数$b$,并将损失函数改写为
$$ \tilde{\mathcal{L}}(\boldsymbol{\theta}) = |\mathcal{L}(\boldsymbol{\theta}) -b| + b\tag{1} $$
其中,$b$是预先设定的阈值,当$\mathcal{L}(\boldsymbol{\theta})>b$时$\tilde{\mathcal{L}}(\boldsymbol{\theta})=\mathcal{L}(\boldsymbol{\theta})$,这时就是执行普通的梯度下降;而$\mathcal{L}(\boldsymbol{\theta})<b$时$\tilde{\mathcal{L}}(\boldsymbol{\theta})=2b-\mathcal{L}(\boldsymbol{\theta})$,注意到损失函数变号了,所以这时候是梯度上升。因此,总的来说就是以$b$为阈值,低于阈值时反而希望损失函数变大。论文把这个改动称为"Flooding"
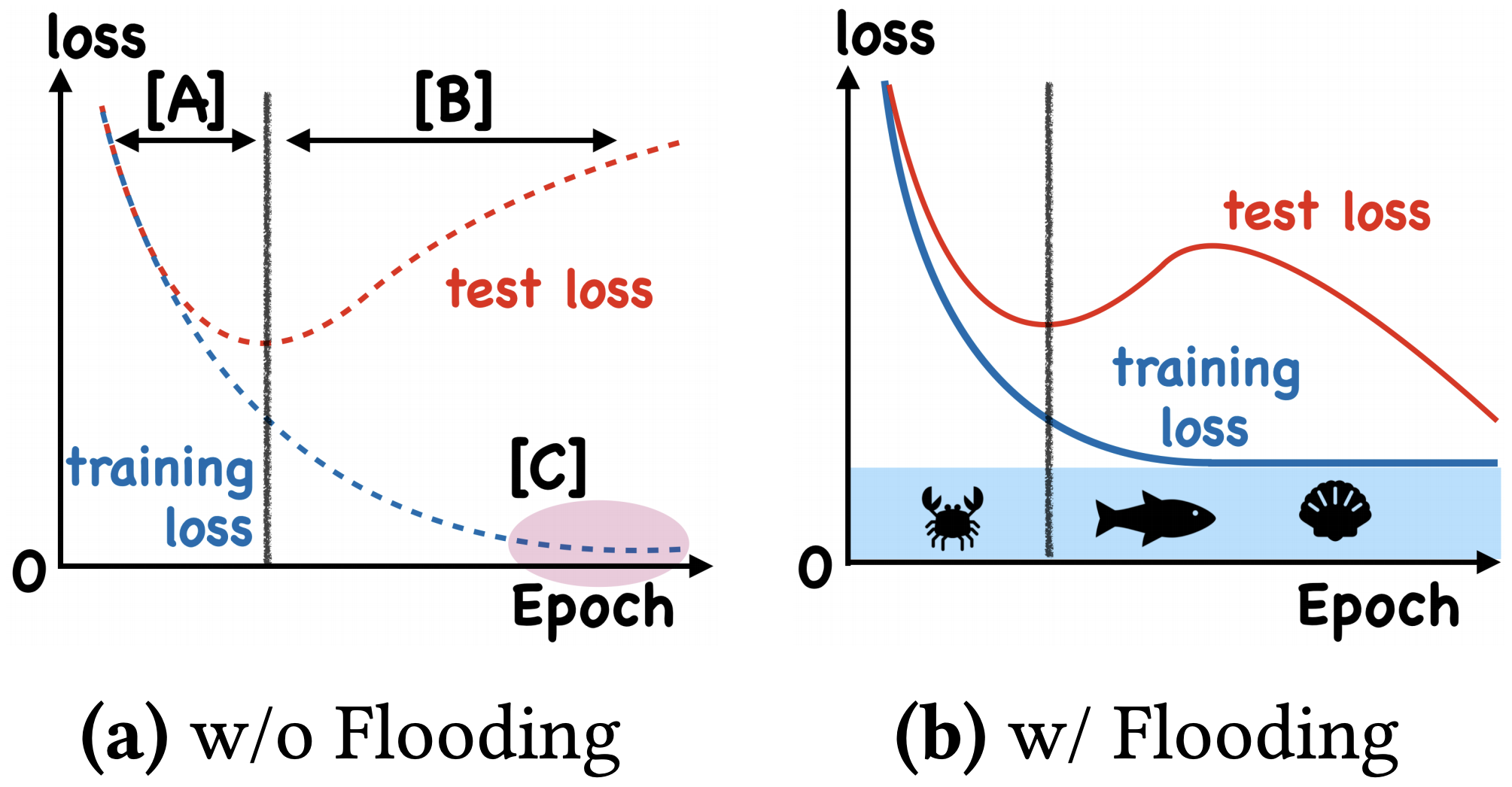
这样做有什么效果呢?论文显示,在某些任务中,训练集的损失函数经过这样处理后,验证集的损失能出现 "二次下降(Double Descent)",如下图
我们可以假设梯度先下降一步后上升一步,学习率为$\varepsilon$,通过泰勒展开可以得到
$$ \boldsymbol{\theta}_{n+1} \approx \boldsymbol{\theta}_{n-1}-\frac{\varepsilon^2}{2}\nabla_{\boldsymbol{\theta}} ||g(\boldsymbol{\theta}_{n-1})||^2\tag{2} $$
其中,$\boldsymbol{\theta}_{n}$表示第$n$次迭代的参数,$g(\boldsymbol{\theta}_{n-1})=\nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta}_{n-1})$表示损失对参数$\boldsymbol{\theta}_{n-1}$的梯度。式(2)的结果相当于以$\frac{\varepsilon^2}{2}$为学习率、损失函数为梯度惩罚$|g(\boldsymbol{\theta})||^2=||\nabla_{\boldsymbol{\theta}}\mathcal{L}(\boldsymbol{\theta})||^2$的梯度下降
详细的推导过程见《我们真的需要把训练集的损失降到零吗?》
Achilles' Heel of Flooding
Flooding的阿喀琉斯之踵在于超参数$b$,我们需要花非常多的时间寻找最佳的阈值$b$,这并不是一件容易的事
Achilles' Heel(阿喀琉斯之踵)阿喀琉斯是古希腊神话故事中的英雄人物,刀枪不入,唯一的弱点是脚后跟(踵)。后用于来比喻某东西的致命缺陷
下图展示了使用BERT在SST-2数据集上不同的阈值$b$对结果的影响(黄色区域是最佳结果)。可以看出,$b$的设置对结果的影响非常大

Gradient Accordance
ACL2022的投稿有一篇名为《Flooding-X: Improving BERT’s Resistance to Adversarial Attacks via Loss-Restricted Fine-Tuning》的文章,以"梯度一致性"作为开启Flooding的"阀门",而不再采用超参数$b$。具体来说,我们首先定义包含参数$\boldsymbol{\theta}$的模型$f$,考虑一个样本$x$以及真实标签$y$,它们的损失为$\mathcal{L}(f(\boldsymbol{\theta}, x), y)$,损失关于参数的梯度为
$$ \boldsymbol{g} = \nabla_{\boldsymbol{\theta}}\mathcal{L}(f(\boldsymbol{\theta}, x),y)\tag{3} $$
其中,式(3)的负值就是参数$\boldsymbol{\theta}$更新的方向。现在我们考虑两个样本$(x_1,y_1), (x_2,y_2)$的情况,根据上述定义,样本1的梯度为
$$ \boldsymbol{g_1} = \nabla_{\boldsymbol{\theta}}\mathcal{L}(f(\boldsymbol{\theta}, x_1), y_1)\tag{4} $$
对于样本1来说,参数更新所导致的损失变化为
$$ \begin{aligned} \Delta \mathcal{L}_1 = &\mathcal{L}(f(\boldsymbol{\theta} - \varepsilon \boldsymbol{g_1}, x_1), y_1)\\ &- \mathcal{L}(f(\boldsymbol{\theta}, x_1), y_1) \end{aligned}\tag{5} $$
将$f(\boldsymbol{\theta}, x_1)$通过泰勒展开变形得
$$ f(\boldsymbol{\theta}, x_1)\approx f(\boldsymbol{\theta} - \varepsilon\boldsymbol{g_1}, x_1) + \varepsilon \boldsymbol{g_1}\frac{\partial f}{\partial \boldsymbol{\theta}}\tag{6} $$
$$ \frac{f(\boldsymbol{\theta} - \varepsilon\boldsymbol{g_1}, x_1) -f(\boldsymbol{\theta}, x_1)}{\varepsilon \boldsymbol{g_1}}= \frac{\partial f}{\partial \boldsymbol{\theta}} $$
我们将$\varepsilon \boldsymbol{g_1}\frac{\partial f}{\partial \boldsymbol{\theta}}$记作$T(x_1)$,并对$\mathcal{L}(f(\boldsymbol{\theta}, x_1), y_1)$做类似的泰勒展开得
$$ \begin{aligned} \mathcal{L}(&f(\boldsymbol{\theta}, x_1), y_1)\\ &= \mathcal{L}(f(\boldsymbol{\theta} - \varepsilon \boldsymbol{g_1}, x_1) + T(x_1), y_1)\\ &\approx \mathcal{L}(f(\boldsymbol{\theta} - \varepsilon \boldsymbol{g_1}, x_1), y_1)\\ &+\frac{\partial \mathcal{L}}{\partial f}T(x_1) \end{aligned}\tag{7} $$
根据式(6)可以推出第一个等号,约等于是从泰勒展开推导的,具体来说
$$ \frac{\mathcal{L}(A + T(x_1), y_1) -\mathcal{L}(A, y_1)}{T(x_1)} = \mathcal{L}' $$
将式(7)带入式(5)得
$$ \begin{aligned} \Delta \mathcal{L}_1 &\approx -\frac{\partial \mathcal{L}}{\partial f}T(x_1)\\ &=-\varepsilon \boldsymbol{g_1}\frac{\partial \mathcal{L}}{\partial f} \frac{\partial f}{\partial \boldsymbol{\theta}}\\ &=-\varepsilon \boldsymbol{g_1} \cdot \boldsymbol{g_1} \end{aligned}\tag{8} $$
类似的,参数根据样本$(x_1,y_1)$更新后,在样本$(x_2, y_2)$上的损失差为$\Delta \mathcal{L}_2 = -\varepsilon \boldsymbol{g_1}\cdot \boldsymbol{g_2}$
值得注意的是,根据定义,$\Delta \mathcal{L}_1$是负的,因为模型是对于$(x_1,y_1)$更新的,自然就会导致其损失的降低。如果$\Delta \mathcal{L_2}$也是负的,那么在$(x_1, y_1)$上更新的模型被认为对$(x_2, y_2)$有积极的影响。上面的等式表明,这种共同关系相当于两个样本的梯度$\boldsymbol{g_1},\boldsymbol{g_2}$之间的乘积,我们称其为梯度一致性(Gradient Accordance)
Coarse-Grained Gradient Accordance
上面提到的可以看作是样本级别的梯度一致性,由于其粒度太细,计算起来非常复杂,因此我们将其应用到batch级别的粗粒度上进行计算
考虑训练过程中包含$n$个样本的mini-batch $B_0$,其中样本$\boldsymbol{X} = \{x_1, x_2,...,x_n\}$,标签$\boldsymbol{y}=\{y_1, y_2,...,y_n\}$,其中$y_i\in \{c_1, c_2,...,c_k\}$,即有$k$个类别。这些样本可以根据它们的标签拆分成$k$组(每组内的样本标签是一样的)
$$ \boldsymbol{X} = \boldsymbol{X_1}\cup \boldsymbol{X_2} \cup \cdots \cup \boldsymbol{X_k} $$
由此可以将$B_0$拆分成多个子batch的并集,$B_0 = B_0^1\cup B_0^2\cup \cdots B_0^k$。我们定义两个子batch $B_0^1$和$B_0^2$的类一致性分数为
$$ C(B_0^1, B_0^2) = \mathbb{E}[\cos (\boldsymbol{g_1}, \boldsymbol{g_2})]\tag{9} $$
其中,$\boldsymbol{g}_1$是模型在样本集$B_0^1$上的损失对参数的梯度,$\cos(\boldsymbol{g_1}, \boldsymbol{g_2})=(\boldsymbol{g_1}/|\boldsymbol{g_1}|)\cdot (\boldsymbol{g_2}/|\boldsymbol{g_2}|)$
类一致性可以用于判断:对类别$c_1$的样本集$B_0^1$进行梯度下降是否也会减少类别$c_2$所对应的样本集$B_0^2$的损失
假设一个Epoch中有$N$个batch,那么$B_s$与$B_t$的批一致性分数定义如下:
$$ \begin{aligned} S_{\text{batch accd}}&(B_s, B_t)\\ &=\frac{1}{k(k-1)}\sum_{j=1}^k\sum_{i=1 \atop i \neq j}^k C(B_s^i, B_t^j) \end{aligned}\tag{10} $$
批一致性可以通过评估一个批次的参数更新对另一个批次的影响,量化两个批次的学习一致性。更具体地说,$S_{\text{batch accd}}$如果是正的,表示这两个批次处于相同的学习节奏下,每个批次更新的模型对它们都有好处
任意一个Epoch的梯度一致性最终定义为
$$ \begin{aligned} &S_{\text{epoch accd}} \\ &= \frac{1}{N(N-1)}\sum_{j=i+1}^N \sum_{i=1}^{N-1} S_{\text{batch accd}}(B_s, B_t) \end{aligned}\tag{11} $$
Analysis and Discussion
实验结果这里就不放了,简单说一下就是作者使用了TextFooler、BERT-Attack、TextBugger三种攻击手段,以PGD、FreeLB、TAVAT等方法为Baseline进行对比,结果表明使用Flooding-X效果很好
从下图可以看出,当梯度一致性指标从负数变为正数时,测试集损失也开始上升,说明梯度一致性这个指标可以很好的当作是过拟合的信号

个人总结
2020年提出的Flooding本身就是一个非常有意思的Trick,可惜原论文作者也苦于超参数$b$的选择,因此其应用不算广泛。ACL2022这篇论文提出了梯度一致性的概念,让模型自己感知什么时候该进行Flooding,避免了超参数的选择问题

请问公式(6)的f'(θ)是否应为负号呢
抱歉我的想法有误,f(x+(-Δx))/-Δx就如您写的那样,十分抱歉