Trie树实现搜索引擎自动联想

源码：https://github.com/wmathor/Search-engine-automatic-association

算法应用背景

我们在使用搜索引擎的时候，只输入一部分关键字，它就会自动将包含该关键字的所有词条罗列出来供你选择

再比方说，我想在淘宝搜索一本有关java的书籍，只需要输入java，搜索框就会自动罗列出有关java的内容，其中就包含了一些java书籍

从上面两个例子可以看出，搜索引擎自动联想功能十分方便，而且很多地方必备这些功能

Trie树（字典树）算法

Trie树又被称为前缀树或者字典树。它的基本作用是用来存储一个字符串集合：{$W_1$, $W_2$, $W_3$, … $W_N$}，并且可以用来查询一个字符串S是不是在集合里

具体来说，Trie 一般支持两个操作：

1. Trie.insert(W)：第一个操作是插入操作，就是将一个字符串 W 加入到集合中
2. Trie.search(S)：第二个操作是查询操作，就是查询一个字符串 S 是不是在集合中

由于 Trie 的特性，它还特别适合处理一些与前缀有关的查询，比如集合中有几个字符串与S 有公共前缀这样的查询

首先我们来看一下 Trie 长什么样子：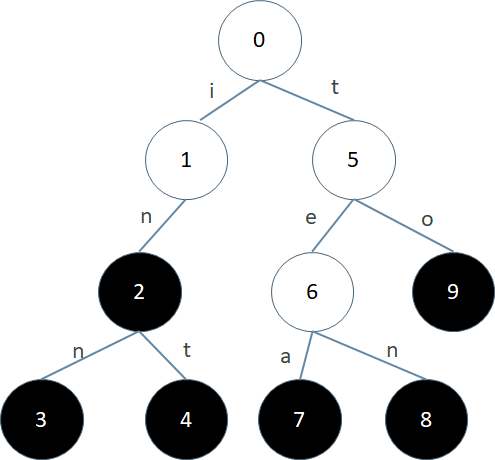

上面这棵 Trie 树包含的字符串集合是 {in, inn, int, tea, ten, to}。每个节点的编号是我们为了描述方便加上去的。树中的每一条边上都标识有一个字符。这些字符可以是任意一个字符集中的字符。比如对于都是小写字母的字符串，字符集就是'a'-'z'；对于都是数字的字符串，字符集就是'0'-'9'；对于二进制字符串，字符集就是 0 和 1

从一个节点连出去的边都必须标识不同的字符。所以一个节点最多有 | 字符集 | 这么多子节点。其中有一些节点是终结点，我们用黑色表示。对于每一个终结点，如果我们把从根到它的路径上的字符按顺序连起来，就对应着一个集合中的字符串

比如上图中 3 号节点对应的路径 0123 上的字符串是 inn，8 号节点对应的路径 0568 上的字符串是 ten。终结点与集合中的字符串是一一对应的

TRIE 插入

假设我们要插入字符串"in"。我们一开始位于根，也就是 0 号节点，我们用 P=0 表示。我们先看 P 是不是有一条标识着"i"的连向子节点的边。没有这条边，于是我们就新建一个节点，也就是 1 号节点，然后把 1 号节点设置为 P 也就是 0 号节点的子节点，并且将边标识为 "i"。最后我们移动到 1 号节点，也就是令 P=1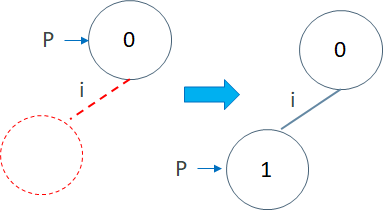

这样我们就把"in"的"i"字符插入到 Trie 中了

然后我们再插入字符"n"，先找 P 也就是 1 号节点有没有标记为"n" 的边。还是没有，于是再新建一个节点 2，设置为 P 也就是 1 号节点的子节点，并且把边标识为 "n"。最后再移动到 P=2。这样我们就把"n"也插入了。由于"n"是"in" 的最后一个字符，所以我们还需要将 P=2 这个节点标记为终结点

现在我们再插入字符串"inn"。过程也是一样的，从 P=0 开始找标识为"i"的边，这次找到 1 号节点。于是我们就不用创建新节点了，直接移动到 1 号节点，也就是令 P=1。再插入字符"n"，也是有 2 号节点存在，所以移动到 2 号节点，P=2。最后再插入字符"n"这时 P 没有标识为"n"的边了，所以新建 3 号节点作为 2 号节点的子节点，边标识为"n"，同时将 3 号节点标记为终结点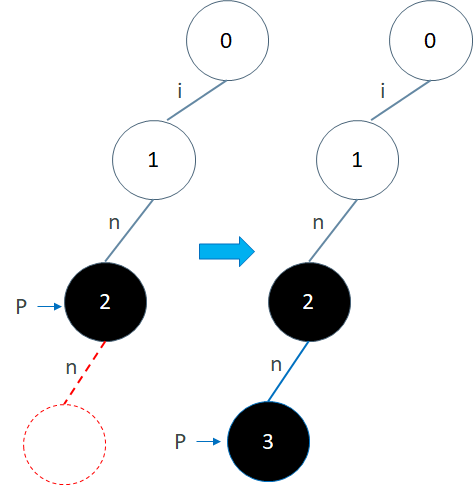

综上所述，在 Trie 中插入一个字符串$W$ 的伪代码如下：

Insert(W):
    P = root
    For i = 1...W.len
        If P.thru(W[i]) == NULL//没有标识为W[i]的边
            P.addChild(W[i],new Node())
        P = p.thru(W[i])
    P.markEndPoint()//标记P为终结点

TRIE 查找

查找其实比较简单。只要从根节点开始，沿着标识着 S[1] -> S[2] -> S[3] … -> S[S.len] 的边移动，如果最后成功到达一个终结点，就说明 S 在 Trie 树中；如果最后无路可走，或者到达一个不是终结点的节点，就说明 S 不在 Trie 树中

比如上图中查找"inn"，就会从 0 号节点经过 1 号节点和 2 号节点，最后到达 3 号节点。3 号节点是终结点，所以"inn"在 Trie 树中。再比如查找 "ten"，就会从 0 号节点，经过 56 到达 8 号节点。8 号节点也是终结点，所以"ten"也在 Trie 树中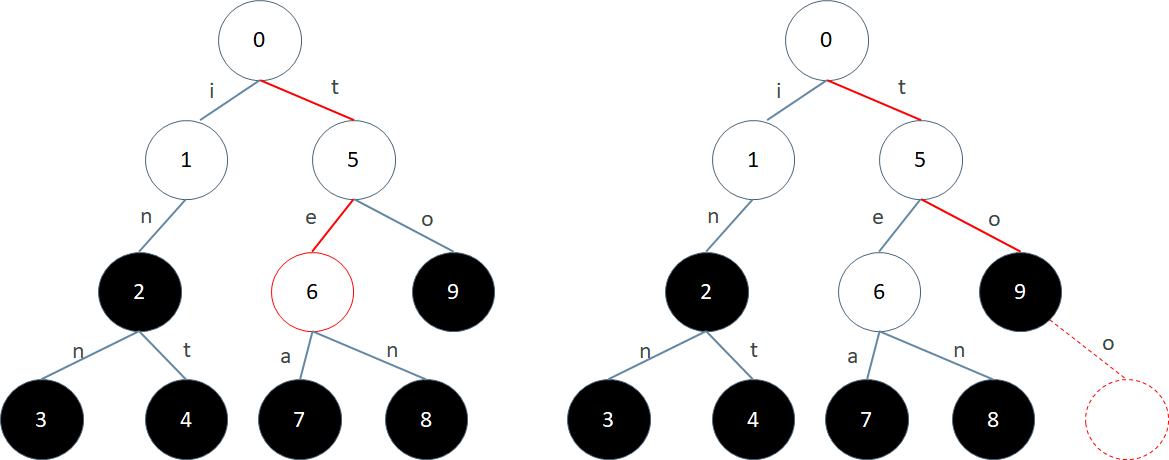

如果是查找"te"，就会从 0 开始经过 5 最后到达 6。但是 6 不是终结点，所以"te"没在 Trie 树中。如果查找的是"too"，就会从 0 开始经过 5 和 9，然后发现之后无路可走：9 号节点没有标记为 o 的边连出去。所以"too"也不在 Trie 中

综上所述，在 Trie 树中查找一个字符串的伪代码如下：

Search(S):
    P = root
    For i = 1...S.len
        If P.thru(S[i]) == NULL
            Return FALSE
        P = P.thru(S[i])
    Return TRUE

实际设计

在设计算法之前，首先准备一个词库，里面包含了要查询的内容


在访问页面的时候首先让Trie读入数据库中的所有内容，对每一条记录依次进行insert操作

class Node {
    public Map<String, Node> nexts; // 子节点
    public int end;
    public Node() {
        this.nexts = new HashMap<String, Node>();
        this.end = 0;
    }
}
Node root = new Node();

public void insert(String word) {
    if (word == null)
        return;
    Node node = root;
    for (int i = 0; i < word.length(); i++) {
        String str = "" + word.charAt(i);
        if (node.nexts.get(str) == null)
            node.nexts.put(str, new Node());
        node = node.nexts.get(str);
    }
    node.end = 1;
}

当Trie树建好之后，整体结果如下图所示：

当系统获取输入框的值后，首先调用Trie树的StartWith方法，查看是否有以当前值为前缀的内容，如果没有就直接返回空，如果有，就需要进行DFS遍历，将以当前值作为前缀的所有值全部查询出来，然后返回给页面

public boolean startWith(String preWord) {
    Node node = root;
    for (int i = 0; i < preWord.length(); i++) {
        String str = "" + preWord.charAt(i);
        if (node.nexts.get(str) == null)
            return false;
        node = node.nexts.get(str);
    }
    return true;
}
List<String> list = new ArrayList<String>();

public List<String> getData(String preword) {
    list.clear();
    if (!startWith(preword))
        return null;
    else {
        StringBuilder str = new StringBuilder("");
        str.append(preword);
        Node node = root;
        for (int i = 0; i < preword.length(); i++)
            node = node.nexts.get("" + preword.charAt(i));
        dfs(node, str);
    }
    return list;
}

private void dfs(Node root, StringBuilder str) {
    if (root.end == 1) {
        list.add(str.toString());
        if (root.nexts.size() == 0)
            return;
    }
    Node node = root;
    for (String s : node.nexts.keySet()) {
        str.append(s);
        dfs(node.nexts.get(s), str);
        str.delete(str.length() - 1, str.length());
    }
}

最终效果展示