一、移位运算展开目录
1. 移位运算的数学意义展开目录
2. 算术移位运算规则展开目录
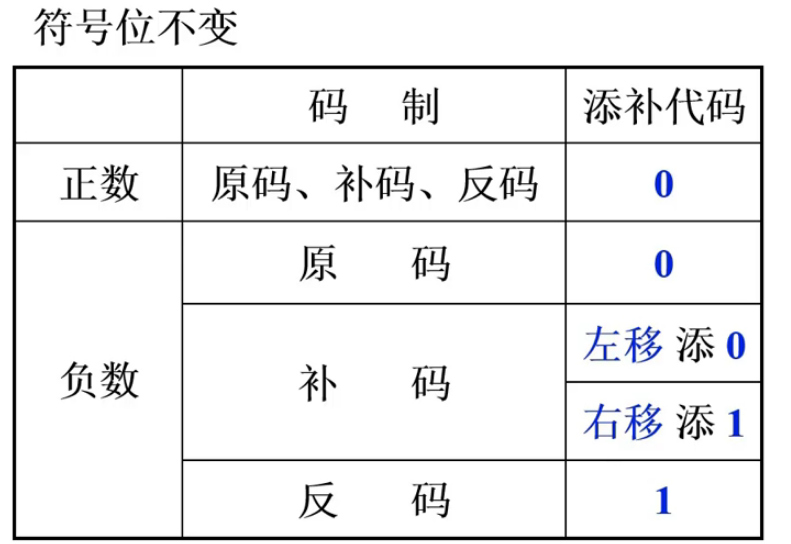设机器数字长为 8 位（含 1 位符号位），写出 A=+26 时，三种机器数左、右移一位和两位后的表示形式及对应的真值，并分析结果的正确性。
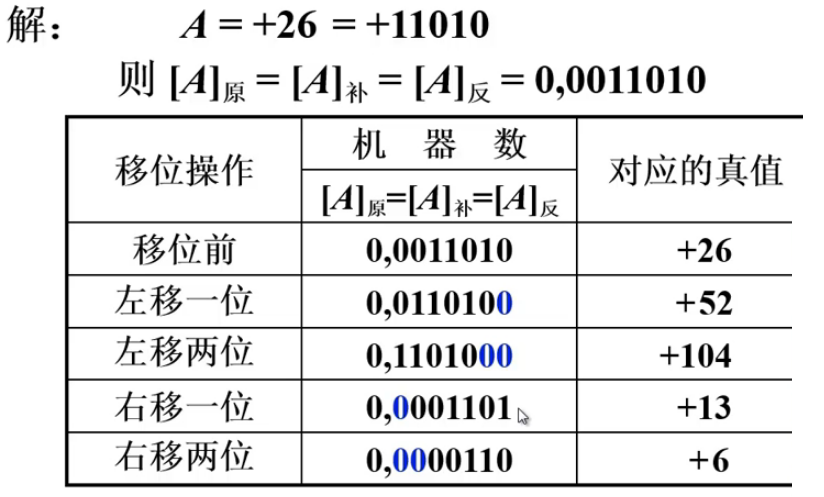设机器数字长为 8 位（含 1 位符号位），写出 A=-26 时，三种机器数左、右移一位和两位后的表示形式及对应的真值，并分析结果的正确性。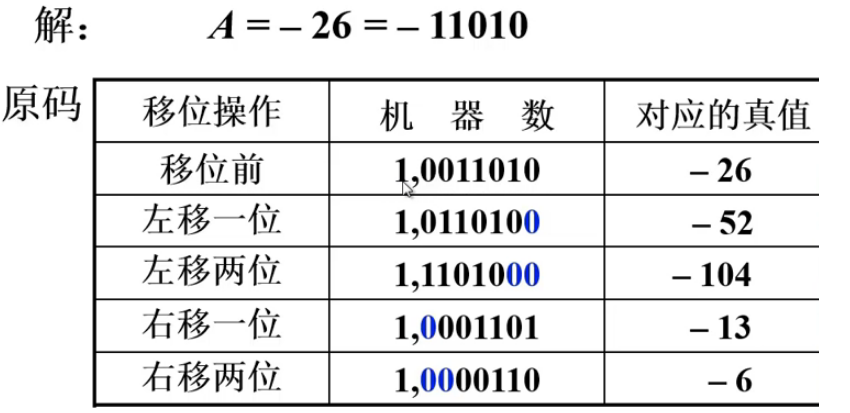
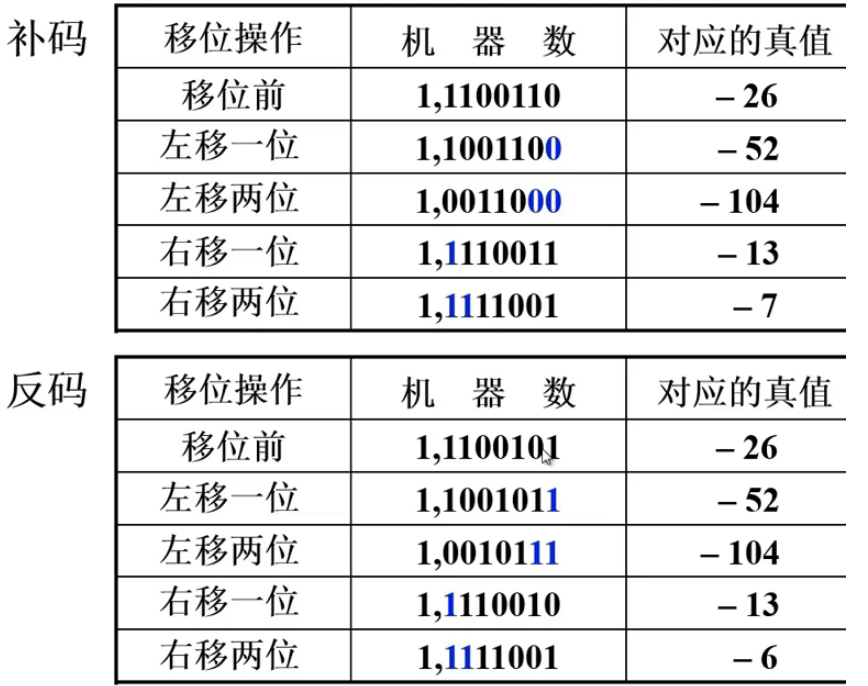
3. 算术移位和逻辑移位的区别展开目录
二、加减法运算展开目录
1. 补码加减运算公式展开目录
2. 举例展开目录
3. 溢出判断展开目录
（1）一位符号位判溢出展开目录
参加操作的两个数（减法时即为被减数和 “求补” 以后的减数）符号为相同，其结果的符号与源操作数的符号不同，即为溢出
（2）两位符号位判溢出展开目录
三、乘法运算展开目录
1. 分析笔算乘法展开目录
若计算机完全模仿笔算乘法步骤，将会有两大困难：其一，将四个位积一次相加，机器难以实现；其二，乘积位数增长了一倍，这将造成器材的浪费和运算时间的增加。
2. 笔算乘法改进展开目录
由上式可见，两数相乘的过程，可视作加法和移位两种运算，这对计算机来说是非常容易实现的
3. 原码乘法展开目录
示例：
4. 补码乘法展开目录
补码乘法比较简单：
- 符号位单独异或运算
- 尾数部分绝对值相乘
5. 例题展开目录
用原码阵列乘法器、补码阵列乘法器分别计算 x*y
（1）x=11011，y=-11111
（2）x=-01011，y=11001
四、除法运算展开目录
暂时用不到，所以不写
