1.什么是决策树
决策树是一种树形结构,为人们提供决策依据,决策树可以用来回答yes和no问题,它通过树形结构将各种情况组合都表示出来,每个分支表示一次选择(选择yes还是no),直到所有选择都进行完毕,最终给出正确答案。
第一个例子
想象一个母亲要给这个女儿介绍男朋友,于是有了下面的对话:
女儿:多大年纪了?
母亲:26。
女儿:长的帅不帅?
母亲:挺帅的。
女儿:收入高不?
母亲:不算很高,中等情况。
女儿:是公务员不?
母亲:是,在税务局上班呢。
女儿:那好,我去见见。
这个女孩的决策过程就是典型的分类树决策。相当于通过年龄、长相、收入和是否公务员对将男人分为两个类别:见和不见。假设这个女孩对男人的要求是:30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员,那么这个可以用下图表示女孩的决策逻辑:
第二个例子
小王想通过下周天气预报预测什么时候人们会打高尔夫,他了解到人们决定是否打球的原因最主要取决于天气情况,天气情况由天气状况、相对湿度、有无风四个方面构成。天气状况有晴、云和雨;相对湿度分大于70、小于等于70。如此,我们便可以构造一棵决策树
上述决策树对应如下表达式:
(Outlook = Sunny && Humidity <= 70) || (Outlook = Overcast) || (Outlook = Rain && Wind = FALSE)2.香农熵

香农熵(entropy),简称熵,由美国数学家、信息论的创始人香农提出。用来定量表示信息的聚合程度,是信息的期望值。
划分数据集的大原则是:将无序的数据变得更加有序。
世界本来是充满各种杂乱信息的,但是被人类不停地认识到,认识的过程还是循序渐进的。原本杂乱的信息却被我们系统地组织起来了,这就要归功于分类了。
学语文时,我们学习白话文,文言文,诗歌,唐诗,宋词,散文,杂文,小说,等等。
学数学时,加减乘除,指数,对数,方程,几何,微积分,概率论,图论,线性,离散,等等。
学英语时,名词,动词,形容词,副词,口语,语法,时态,等等。
学历史时,中国史,世界史,原始社会,奴隶社会,封建社会,现代社会,等等。
分类分的越好,我们理解,掌握起来就会更轻松。并且一个新事物出现,我们可以基于已经学习到的经验预测到它大概是什么。
熵就是用来描述信息的这种确定与不确定状态的,信息越混乱,熵越大,信息分类越清晰,熵越小。
我们来看一个例子,马上要举行世界杯赛了。大家都很关心谁会是冠军。假如我错过了看世界杯,赛后我问一个知道比赛结果的观众“哪支球队是冠军”? 他不愿意直接告诉我, 而要让我猜,并且我每猜一次,他要收一元钱才肯告诉我是否猜对了,那么我需要付给他多少钱才能知道谁是冠军呢? 我可以把球队编上号,从 1 到 32, 然后提问: “冠军的球队在 1-16 号中吗?” 假如他告诉我猜对了, 我会接着问: “冠军在 1-8 号中吗?” 假如他告诉我猜错了, 我自然知道冠军队在 9-16 中。 这样最多只需要五次, 我就能知道哪支球队是冠军。所以,谁是世界杯冠军这条消息的信息量只值五块钱。(球队第一种分类方式)
我们实际上可能不需要猜五次就能猜出谁是冠军,因为像巴西、德国、意大利这样的球队得冠军的可能性比日本、美国、韩国等队大的多。因此,我们第一次猜测时不需要把 32 个球队等分成两个组,而可以把少数几个最可能的球队分成一组,把其它队分成另一组。然后我们猜冠军球队是否在那几只热门队中。我们重复这样的过程,根据夺冠概率对剩下的候选球队分组,直到找到冠军队。这样,我们也许三次或四次就猜出结果。因此,当每个球队夺冠的可能性(概率)不等时,“谁获得世界杯冠军”的信息量就比五块钱少。(球队第二种分类方式)
熵定义为信息的期望值。求得熵,需要先知道信息的定义。如果待分类的事务可以划分在多个分类之中,则信息定义为
$$l(x_i)= - log_2 p(x_i) \tag{公式1}$$
其中,$x_i$表示第$i$个分类,$p(xi)$表示选择第$i$个分类的概率。
假如有变量$X$,其可能的分类有$n$种,$X$的熵可以通过下面的公式得到:
$$H(X)=-\sum_{i=1}^n p(x_i) log_2 p(x_i) \tag{公式2}$$
以上面球队为例,第一种分类的话,所得球队的熵为:
$$ \begin{align} H & = -\sum_{i=1}^n p(x_i) log_2 p(x_i) \\ & = -\left(\frac{1}{32}\log_2 \frac{1}{32}\right)\times32 \\ & = -\log_2 \frac{1}{32} \\ & = -\log_2 32^{-1} \\ & = \log_2 32 \\ & = 5(次) \end{align} $$
如果是按第二种方式分类的话,假如,每个队得冠军的概率是这样的
| 球队 | 分类 | 获胜概率 |
|---|---|---|
| 中国 | 强队 | 18% |
| 巴西 | 强队 | 18% |
| 德国 | 强队 | 18% |
| 意大利 | 强队 | 18% |
| 剩下的28只球队每队获胜概率都为1% | 弱队 | 1% |
现在分成了两个队强队和弱队,需要分别计算两队的熵,然后再计算总的熵。
强队的熵为:
$$ \begin{align} H & = -\sum_{i=1}^n p(x_i) log_2 p(x_i) \\ & = -\left(\frac{1}{4}\log_2 \frac{1}{4}\right)\times4 \\ & = -\log_2 \frac{1}{4} \\ & = -\log_2 4^{-1} \\ & = \log_2 4 \\ & = 2(次) \end{align} $$
弱队的熵为:
$$ \begin{align} H & = -\sum_{i=1}^n p(x_i) log_2 p(x_i) \\ & = -\left(\frac{1}{28}\log_2 \frac{1}{28}\right)\times28 \\ & = -\log_2 \frac{1}{28} \\ & = -\log_2 28^{-1} \\ & = \log_2 28 \\ & \approx 4.8(次) \end{align} $$
所得球队的总的熵为:
$$ \begin{align} H & = 0.72\times2+0.28\times4.8 \\ & \approx 2.784(次) \end{align} $$
可以看到,如果我们按照强弱队的方式来分类,然后再猜的话,平均只需要2.8次就可以猜出冠军球队。
3.信息增益
信息增益(information gain)指的是划分数据集前后信息发生的变化。
在信息增益中,衡量标准是看特征能够为分类系统带来多少信息,带来的信息越多,该特征越重要。对一个特征而言,系统有它和没它时信息量将发生变化,而前后信息量的差值就是这个特征给系统带来的信息量。所谓信息量,就是熵。
特征T给聚类C或分类C带来的信息增益可以定义为
$$IG(T)=H(C)-H(C|T) \tag{公式3}$$
其中,$IG(T)$表示特征$T$带来的信息增益,$H(C)$表示未使用特征$T$时的熵,$H(C|T)$表示使用特征$T$时的熵。并且$H(C)$一定会大于等于$H(C|T)$。
例如,上面的球队按第一种分类得到的熵为 5,第二种分类得到的熵为 2.8,则强弱队这个特征为 32 只球队带来的信息增益则为:5-2.8=2.2 。
信息增益最大的问题在于它只能考察特征对整个系统的贡献,而不能具体到某个类别上,这就使得它只适合用来做所谓“全局”的特征选择。
一个特征带来的信息增益越大,越适合用来做分类的特征。
4.构造决策树
现在统计了14天的气象数据(指标包括outlook,temperature,humidity,windy),并已知这些天气是否打球(play)。如果给出新一天的气象指标数据:sunny,cool,high,TRUE,判断一下会不会去打球。
| outlook | temperature | humidity | windy | play |
|---|---|---|---|---|
| sunny | hot | high | FALSE | no |
| sunny | hot | high | TRUE | no |
| overcast | hot | high | FALSE | yes |
| rainy | mild | high | FALSE | yes |
| rainy | cool | normal | FALSE | yes |
| rainy | cool | normal | TRUE | no |
| overcast | cool | normal | TRUE | yes |
| sunny | mild | high | FALSE | no |
| sunny | cool | normal | FALSE | yes |
| rainy | mild | normal | FALSE | yes |
| sunny | mild | normal | TRUE | yes |
| overcast | mild | high | TRUE | yes |
| overcast | hot | normal | FALSE | yes |
| rainy | mild | high | TRUE | no |
ID3算法
构造树的基本想法是随着树深度的增加,节点的熵迅速地降低。熵降低的速度越快越好(即信息增益越大越好),这样我们有望得到一棵高度最矮的决策树。
好,现在用此算法来分析天气的例子。
在没有使用任何特征情况下。根据历史数据,我们只知道新的一天打球的概率是$\frac{9}{14}$,不打的概率是$\frac{5}{14}$。此时的熵为:
$$ \begin{align} H & = -\sum_{i=1}^n p(x_i) log_2 p(x_i) \\ & = -\left(\frac {5}{14} \log_2 \frac{5}{14}+\frac{9}{14}\log_2 \frac{9}{14}\right) \\ & \approx -\left(0.357\times(-1.486)+0.643\times(-0.637)\right) \\ & \approx 0.940 \end{align} $$
如果按照每个特征分类的话。属性有4个:outlook,temperature,humidity,windy。我们首先要决定哪个属性作树的根节点。
对每项指标分别统计:在不同的取值下打球和不打球的次数。
| outlook | yes | no |
|---|---|---|
| sunny | 2 | 3 |
| overcast | 4 | 0 |
| rainy | 3 | 2 |
$$ \begin{align} H(sunny ) & = -\sum_{i=1}^n p(x_i) log_2 p(x_i) \\ & = -\left(\frac {2}{5} \log_2 \frac{2}{5}+\frac{3}{5}\log_2 \frac{3}{5}\right) \\ & \approx 0.971 \end{align} $$
$$ \begin{align} H(overcast) & = -\sum_{i=1}^n p(x_i) log_2 p(x_i) \\ & = -\left(\log_2 {1}\right) \\ & =0 \end{align} $$
$$ \begin{align} H(rainy) & = -\sum_{i=1}^n p(x_i) log_2 p(x_i) \\ & = -\left(\frac {3}{5} \log_2 \frac{3}{5}+\frac{2}{5}\log_2 \frac{2}{5}\right) \\ & \approx 0.971 \end{align} $$
因此如果用特征outlook来分类的话,总的熵为
$$ \begin{align} H(outlook ) & = \frac {5}{14} \times0.971+0+ \frac {5}{14} \times0.971\\ & \approx 0.714\times0.971 \\ & \approx 0.694 \end{align} $$
然后,求得特征outlook获得的信息增益。
$$IG(outlook )=0.940-0.694=0.246 \tag{outlook的信息增益 }$$
用同样的方法,可以分别求出$temperature$,$humidity$,$windy$的信息增益。$IG(temperature)=0.029$,$IG(humidity)=0.152$,$IG(windy)=0.048$。
因为$IG(outlook)>IG(humidity)>IG(windy)>IG(temperature)$。所以根节点应该选择$outlook$特征来进行分类。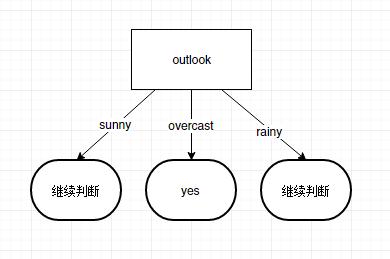
接下来要继续判断取$temperature$、$humidity$还是$windy$?在已知$outlook=sunny$的情况,根据历史数据,分别计算$IG(temperature)$、$IG(humidity)$和$IG(windy)$,选最大者为特征。
依此类推,构造决策树。当系统的信息熵降为0时,就没有必要再往下构造决策树了,此时叶子节点都是纯的–这是理想情况。最坏的情况下,决策树的高度为属性(决策变量)的个数,叶子节点不纯(这意味着我们要以一定的概率来作出决策,一般采用多数表决的方式确定此叶子节点)
构造决策树的一般过程
- 收集数据:可以使用任何方法。
- 准备数据:树构造算法只适用于标称型数据,因此数值型数据必须离散化。
- 分析数据:可以使用任何方法,构造树完成之后,我们应该检查图形是否符合预期。
- 训练算法:构造树的数据结构。
- 测试算法:使用经验树计算错误率。
- 使用算法:此步骤可以适用于任何监督学习算法,而使用决策树可以更好地理解数据的内在含义。
Java实现
定义数据结构
根据决策树的形状,我将决策树的数据结构定义如下。lastFeatureValue表示经过某个特征值的筛选到达的节点,featureName表示答案或者信息增益最大的特征。childrenNodeList表示经过这个特征的若干个值分类后得到的几个节点
public class Node {
/**
* 到达此节点的特征值
*/
public String lastFeatureValue;
/**
* 此节点的特征名称或答案
*/
public String featureName;
/**
* 此节点的分类子节点
*/
public List<Node> childrenNodeList = new ArrayList<Node>();
}定义输入数据格式
文章最开始抛出的问题中的数据的输入格式是这样的
@feature
outlook,temperature,humidity,windy,play
@data
sunny,hot,high,FALSE,no
sunny,hot,high,TRUE,no
overcast,hot,high,FALSE,yes
rainy,mild,high,FALSE,yes
rainy,cool,normal,FALSE,yes
rainy,cool,normal,TRUE,no
overcast,cool,normal,TRUE,yes
sunny,mild,high,FALSE,no
sunny,cool,normal,FALSE,yes
rainy,mild,normal,FALSE,yes
sunny,mild,normal,TRUE,yes
overcast,mild,high,TRUE,yes
overcast,hot,normal,FALSE,yes
rainy,mild,high,TRUE,no存储输入数据
在代码中,特征和特征值用List来存储,数据用Map来存储
//特征列表
public static List<String> featureList = new ArrayList<String>();
// 特征值列表
public static List<List<String>> featureValueTableList = new ArrayList<List<String>>();
//得到全局数据
public static Map<Integer, List<String>> tableMap = new HashMap<Integer, List<String>>();初始化输入数据
对输入数据进行初始化
/**
* 初始化数据
*
* @param file
*/
public static void readOriginalData( File file )
{
int index = 0;
try
{
FileReader fr = new FileReader( file );
BufferedReader br = new BufferedReader( fr );
String line;
while ( (line = br.readLine() ) != null )
{
/* 得到特征名称 */
if ( line.startsWith( "@feature" ) )
{
line = br.readLine();
String[] row = line.split( "," );
for ( String s : row )
{
featureList.add( s.trim() );
}
}else if ( line.startsWith( "@data" ) )
{
while ( (line = br.readLine() ) != null )
{
if ( line.equals( "" ) )
{
continue;
}
String[] row = line.split( "," );
if ( row.length != featureList.size() )
{
throw new Exception( "列表数据和特征数目不一致" );
}
List<String> tempList = new ArrayList<String>();
for ( String s : row )
{
if ( s.trim().equals( "" ) )
{
throw new Exception( "列表数据不能为空" );
}
tempList.add( s.trim() );
}
tableMap.put( index++, tempList );
}
/* 遍历tableMap得到属性值列表 */
Map<Integer, Set<String> > valueSetMap = new HashMap<Integer, Set<String> >();
for ( int i = 0; i < featureList.size(); i++ )
{
valueSetMap.put( i, new HashSet<String>() );
}
for ( Map.Entry<Integer, List<String> > entry : tableMap.entrySet() )
{
List<String> dataList = entry.getValue();
for ( int i = 0; i < dataList.size(); i++ )
{
valueSetMap.get( i ).add( dataList.get( i ) );
}
}
for ( Map.Entry<Integer, Set<String> > entry : valueSetMap.entrySet() )
{
List<String> valueList = new ArrayList<String>();
for ( String s : entry.getValue() )
{
valueList.add( s );
}
featureValueTableList.add( valueList );
}
}else {
continue;
}
}
br.close();
}
catch ( IOException e1 )
{
e1.printStackTrace();
}
catch ( Exception e )
{
e.printStackTrace();
}
}计算给定数据集的香农熵
/**
* 计算熵
*
* @param dataSetList
* @return
*/
public static double calculateEntropy( List<Integer> dataSetList )
{
if ( dataSetList == null || dataSetList.size() <= 0 )
{
return(0);
}
/* 得到结果 */
int resultIndex = tableMap.get( dataSetList.get( 0 ) ).size() - 1;
Map<String, Integer> valueMap = new HashMap<String, Integer>();
for ( Integer id : dataSetList )
{
String value = tableMap.get( id ).get( resultIndex );
Integer num = valueMap.get( value );
if ( num == null || num == 0 )
{
num = 0;
}
valueMap.put( value, num + 1 );
}
double entropy = 0;
for ( Map.Entry<String, Integer> entry : valueMap.entrySet() )
{
double prob = entry.getValue() * 1.0 / dataSetList.size();
entropy -= prob * Math.log10( prob ) / Math.log10( 2 );
}
return(entropy);
}按照给定特征划分数据集
/**
* 对一个数据集进行划分
*
* @param dataSetList
* 待划分的数据集
* @param featureIndex
* 第几个特征(特征下标,从0开始)
* @param value
* 得到某个特征值的数据集
* @return
*/
public static List<Integer> splitDataSet( List<Integer> dataSetList, int featureIndex, String value )
{
List<Integer> resultList = new ArrayList<Integer>();
for ( Integer id : dataSetList )
{
if ( tableMap.get( id ).get( featureIndex ).equals( value ) )
{
resultList.add( id );
}
}
return(resultList);
}选择最好的数据集划分方式
/**
* 在指定的几个特征中选择一个最佳特征(信息增益最大)用于划分数据集
*
* @param dataSetList
* @return 返回最佳特征的下标
*/
public static int chooseBestFeatureToSplit( List<Integer> dataSetList, List<Integer> featureIndexList )
{
double baseEntropy = calculateEntropy( dataSetList );
double bestInformationGain = 0;
int bestFeature = -1;
/* 循环遍历所有特征 */
for ( int temp = 0; temp < featureIndexList.size() - 1; temp++ )
{
int i = featureIndexList.get( temp );
/* 得到特征集合 */
List<String> featureValueList = new ArrayList<String>();
for ( Integer id : dataSetList )
{
String value = tableMap.get( id ).get( i );
featureValueList.add( value );
}
Set<String> featureValueSet = new HashSet<String>();
featureValueSet.addAll( featureValueList );
/* 得到此分类下的熵 */
double newEntropy = 0;
for ( String featureValue : featureValueSet )
{
List<Integer> subDataSetList = splitDataSet( dataSetList, i, featureValue );
double probability = subDataSetList.size() * 1.0 / dataSetList.size();
newEntropy += probability * calculateEntropy( subDataSetList );
}
/* 得到信息增益 */
double informationGain = baseEntropy - newEntropy;
/* 得到信息增益最大的特征下标 */
if ( informationGain > bestInformationGain )
{
bestInformationGain = informationGain;
bestFeature = temp;
}
}
return(bestFeature);
}多数表决不确定结果
如果所有属性都划分完了,答案还没确定,需要通过多数表决的方式得到答案
/**
* 多数表决得到出现次数最多的那个值
*
* @param dataSetList
* @return
*/
public static String majorityVote( List<Integer> dataSetList )
{
/* 得到结果 */
int resultIndex = tableMap.get( dataSetList.get( 0 ) ).size() - 1;
Map<String, Integer> valueMap = new HashMap<String, Integer>();
for ( Integer id : dataSetList )
{
String value = tableMap.get( id ).get( resultIndex );
Integer num = valueMap.get( value );
if ( num == null || num == 0 )
{
num = 0;
}
valueMap.put( value, num + 1 );
}
int maxNum = 0;
String value = "";
for ( Map.Entry<String, Integer> entry : valueMap.entrySet() )
{
if ( entry.getValue() > maxNum )
{
maxNum = entry.getValue();
value = entry.getKey();
}
}
return(value);
}创建决策树
/**
* 创建决策树
*
* @param dataSetList
* 数据集
* @param featureIndexList
* 可用的特征列表
* @param lastFeatureValue
* 到达此节点的上一个特征值
* @return
*/
public static Node createDecisionTree( List<Integer> dataSetList, List<Integer> featureIndexList, String lastFeatureValue )
{
/* 如果只有一个值的话,则直接返回叶子节点 */
int valueIndex = featureIndexList.get( featureIndexList.size() - 1 );
/* 选择第一个值 */
String firstValue = tableMap.get( dataSetList.get( 0 ) ).get( valueIndex );
int firstValueNum = 0;
for ( Integer id : dataSetList )
{
if ( firstValue.equals( tableMap.get( id ).get( valueIndex ) ) )
{
firstValueNum++;
}
}
if ( firstValueNum == dataSetList.size() )
{
Node node = new Node();
node.lastFeatureValue = lastFeatureValue;
node.featureName = firstValue;
node.childrenNodeList = null;
return(node);
}
/* 遍历完所有特征时特征值还没有完全相同,返回多数表决的结果 */
if ( featureIndexList.size() == 1 )
{
Node node = new Node();
node.lastFeatureValue = lastFeatureValue;
node.featureName = majorityVote( dataSetList );
node.childrenNodeList = null;
return(node);
}
/* 获得信息增益最大的特征 */
int bestFeatureIndex = chooseBestFeatureToSplit( dataSetList, featureIndexList );
/* 得到此特征在全局的下标 */
int realFeatureIndex = featureIndexList.get( bestFeatureIndex );
String bestFeatureName = featureList.get( realFeatureIndex );
/* 构造决策树 */
Node node = new Node();
node.lastFeatureValue = lastFeatureValue;
node.featureName = bestFeatureName;
/* 得到所有特征值的集合 */
List<String> featureValueList = featureValueTableList.get( realFeatureIndex );
/* 删除此特征 */
featureIndexList.remove( bestFeatureIndex );
/* 遍历特征所有值,划分数据集,然后递归得到子节点 */
for ( String fv : featureValueList )
{
/* 得到子数据集 */
List<Integer> subDataSetList = splitDataSet( dataSetList, realFeatureIndex, fv );
/* 如果子数据集为空,则使用多数表决给一个答案。 */
if ( subDataSetList == null || subDataSetList.size() <= 0 )
{
Node childNode = new Node();
childNode.lastFeatureValue = fv;
childNode.featureName = majorityVote( dataSetList );
childNode.childrenNodeList = null;
node.childrenNodeList.add( childNode );
break;
}
/* 添加子节点 */
Node childNode = createDecisionTree( subDataSetList, featureIndexList, fv );
node.childrenNodeList.add( childNode );
}
return(node);
}使用决策树对测试数据进行预测
/**
* 输入测试数据得到决策树的预测结果
* @param decisionTree 决策树
* @param featureList 特征列表
* @param testDataList 测试数据
* @return
*/
public static String getDTAnswer( Node decisionTree, List<String> featureList, List<String> testDataList )
{
if ( featureList.size() - 1 != testDataList.size() )
{
System.out.println( "输入数据不完整" );
return("ERROR");
}
while ( decisionTree != null )
{
/* 如果孩子节点为空,则返回此节点答案. */
if ( decisionTree.childrenNodeList == null || decisionTree.childrenNodeList.size() <= 0 )
{
return(decisionTree.featureName);
}
/* 孩子节点不为空,则判断特征值找到子节点 */
for ( int i = 0; i < featureList.size() - 1; i++ )
{
/* 找到当前特征下标 */
if ( featureList.get( i ).equals( decisionTree.featureName ) )
{
/* 得到测试数据特征值 */
String featureValue = testDataList.get( i );
/* 在子节点中找到含有此特征值的节点 */
Node childNode = null;
for ( Node cn : decisionTree.childrenNodeList )
{
if ( cn.lastFeatureValue.equals( featureValue ) )
{
childNode = cn;
break;
}
}
/* 如果没有找到此节点,则说明训练集中没有到这个节点的特征值 */
if ( childNode == null )
{
System.out.println( "没有找到此特征值的数据" );
return("ERROR");
}
decisionTree = childNode;
break;
}
}
}
return("ERROR");
}测试结果
构建的决策树输出是这样的
<?xml version="1.0" encoding="UTF-8" standalone="yes"?>
<Node>
<featureName>outlook</featureName>
<childrenNodeList>
<lastFeatureValue>rainy</lastFeatureValue>
<featureName>windy</featureName>
<childrenNodeList>
<lastFeatureValue>FALSE</lastFeatureValue>
<featureName>yes</featureName>
</childrenNodeList>
<childrenNodeList>
<lastFeatureValue>TRUE</lastFeatureValue>
<featureName>no</featureName>
</childrenNodeList>
</childrenNodeList>
<childrenNodeList>
<lastFeatureValue>sunny</lastFeatureValue>
<featureName>humidity</featureName>
<childrenNodeList>
<lastFeatureValue>normal</lastFeatureValue>
<featureName>yes</featureName>
</childrenNodeList>
<childrenNodeList>
<lastFeatureValue>high</lastFeatureValue>
<featureName>no</featureName>
</childrenNodeList>
</childrenNodeList>
<childrenNodeList>
<lastFeatureValue>overcast</lastFeatureValue>
<featureName>yes</featureName>
</childrenNodeList>
</Node>转换成图是这样的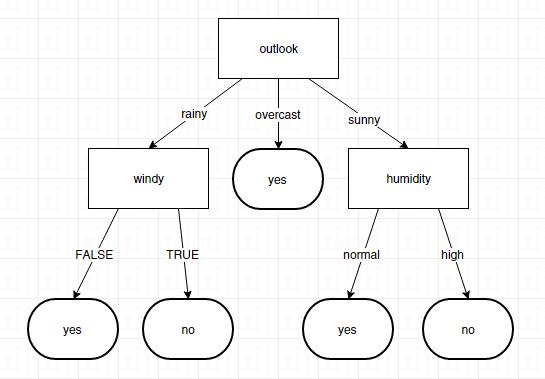
此时输入数据进行测试
rainy,cool,high,TRUE得到结果为:
判断结果:no决策树的优缺点
优点
计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据
缺点
可能会产生过度匹配问题。
当特征和特征值过多时,这些匹配选项可能太多了,我们将这种问题称之为过度匹配(overfitting)。为了减少过度匹配问题,我们可以裁剪决策树,去掉一些不必要的叶子节点。如果叶子节点只能增加少许信息,则可以删除该结点,将它并入到其他叶子节点中去。
另外,对于标称型数据字符串还比较好说,对于数值型数据却无法直接处理,虽然可以将数值型数据划分区间转化为标称型数据,但是如果有很多特征都是数值型数据,还是会比较麻烦。
参考文献
《机器学习实战》(Machine Learning in Action),Peter Harrington著,人民邮电出版社
http://www.cnblogs.com/zhangchaoyang/articles/2196631.html
http://baike.baidu.com/item/%E9%A6%99%E5%86%9C%E7%86%B5
http://www.cnblogs.com/bourneli/archive/2013/03/15/2961568.html
http://www.cnblogs.com/leoo2sk/archive/2010/09/19/decision-tree.html

来了来了@(你懂的)
来了老弟@(你懂的)