并查集（Union Find Set）

并查集概述展开目录

并查集的数学模型是一组不相交的动态集合 S={A,B,...}, 它支持以下运算：

1. union (A,B)：将集合 A 和集合 B 合并
2. find (x)：找出包含元素 x 的集合
3. connected (A,B)：返回 A 和 B 是否连通

我们看一张图来具体说明
开始的情况是对于一个集合 S={0,1,...,9} 他们都是孤立的，随着程序的执行，用户输入不同的操作，比如 union (3,4)，union (3,8) 等等，随着数据的输入，整个图的连通性也会发生变化，所以并查集常常用来解决动态连通性问题

Union-Find API展开目录

上面介绍了并查集的概念，下面我们就要设计并查集。我们现在考虑几种不同的实现，所有的实现都基于使用数组 id [ ] 来确定两个触点是否在同一集合中。以下 API 封装了我们需要的基本操作
分析以上 API，方法 connected 和 union 都依赖于 find，connected 对两个参数调用两次 find 方法，而 union 在真正执行 union 之前也需要判断是否连通，这又是两次调用 find 方法，因此我们需要把 find 方法设计的尽可能高效，所以就有了下面 Quick-Find 实现

Quick-Find 算法：展开目录

class UF {
    private int[] id;
    private int count;
    public UF(int N) {//初始化分量id数组
        count = N;
        id = new int[N];
        for(int i = 0;i < N;i++)
            id[i] = i;
    }
    public int count() {
        return count;
    }
    public boolean connected(int p,int q) {
        return find(p) == find(q);
    }
    public int find(int p) {
        return id[p];
    }
    public void union(int p,int q) {
        int pid = id[p];
        int qid = id[q];
        for(int i = 0;i < id.length;i++) 
            if(id[i] == pid)
                id[i] = qid;
        count--;
    }
}

举个例子，比如输入 union (5,9)，那么首先通过 find 方法发现 id [5] != id [9]，这时 union 函数就会遍历数组，将所有 id [i] 的值为 1 的都改为 8，当然，由 8 改成 1 也行，只要保证每次都采用一种规则就行
上述代码的 find 方法十分高效，但问题也随之而来，设想一下，如果要添加的新路径数量是 M，节点数量是 N，那么时间复杂度就是 O (MN)，这显然是一个平方的复杂度，对于大规模数据而言，这显然是不行的，想要解决这个问题，关键在于提高 union 方法的效率，让他不再需要遍历整个数组

Quick-Union 算法：展开目录

考虑一下，为什么以上的解法会造成 “牵一发而动全身”？因为每个节点所属的组号都是单独记录，各自为政的，没有将它们以更好的方式组织起来，当涉及到修改的时候，除了逐一通知、修改，别无他法。所以现在的问题就变成了，如何将节点以更好的方式组织起来，组织的方式有很多种，但是最直观的还是将组号相同的节点组织在一起，想想所学的数据结构，什么样子的数据结构能够将一些节点给组织起来？常见的就是链表，图，树，什么的了。但是哪种结构对于查找和修改的效率最高？毫无疑问是树，因此考虑如何将节点和组的关系以树的形式表现出来

如果不改变底层数据结构，即不改变使用数组的表示方法的话。可以采用 parent-link 的方式将节点组织起来，举例而言，id [p] 的值就是 p 节点的父节点的序号，如果 p 是树根的话，id [p] 的值就是 p，因此最后经过若干次查找，一个节点总是能够找到它的根节点，即满足 id [root] = root 的节点也就是组的根节点了，然后就可以使用根节点的序号来表示组号。所以在处理一个 pair 的时候，将首先找到 pair 中每一个节点的组号 (即它们所在树的根节点的序号)，如果属于不同的组的话，就将其中一个根节点的父节点设置为另外一个根节点，相当于将一颗独立的树编程另一颗独立的树的子树。直观的过程如下图所示。但是这个时候又引入了问题。
在实现上，其它的方法都一样，只有 find 和 union 这两个方法有所不同

public int find(int p) {
    //根节点具有性质：root = id[root]
    while(p != id[p])
        p = id[p];
    return p;
}
public void union(int p,int q) {
    int pRoot = find(p);
    int qRoot = find(q);
    if(pRoot == qRoot) 
        return;
    id[pRoot] = qroot;//将一个树变成另一棵树的子树
    count--;
}

分析上面代码的时间复杂度我们能发现，主要耗时在 find 上，find 需要不断向上寻找自己的根节点，也就是说，树越长，时间复杂度越高，时间复杂度与树的高度成正比。而树这种数据结构又很容易出现极端情况，如果输入数据是有序的情况，树就会退化为一个链表，如下图所示：
问题已经到这了，思考一下如何优化，回想之前的代码：id[pRoot] = qRoot，p 所在的树总是会作为 q 所在树的子树，那么这种规则是否合理呢？显然不是，比如 p 所在的树的规模比 q 所在树的规模打的多时，p 和 q 结合之后形成的树就是十分不和谐的一头轻一头重的 “畸形树” 了。所以我们应该考虑树的大小，然后再来决定倒是调用：id[pRoot] = qRoot 还是 id[qRoot] = pRoot，即总是 size 小的树作为子树和 size 大的树进行合并，这样就能尽量保持整棵树的平衡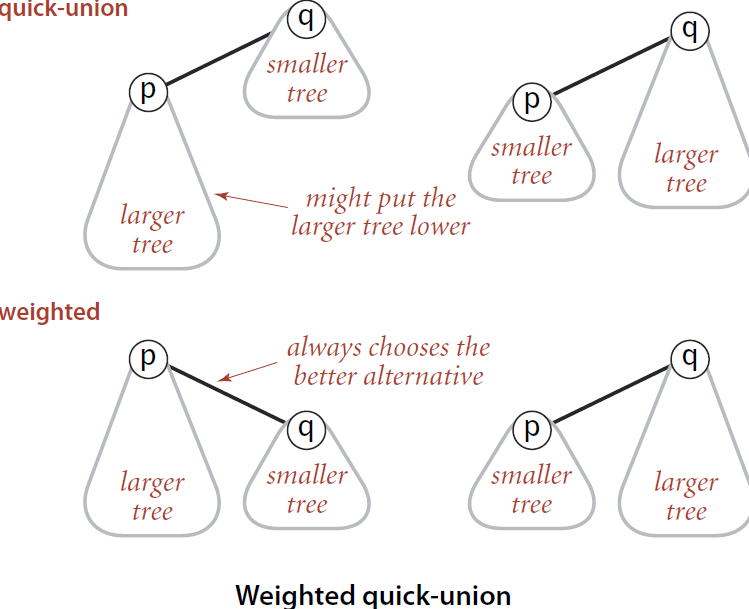
那么现在问题来了，树的大小如何确定？在初始情况下，每个集合的大小都是 1，因为只有自己作为集合，所以我们可以使用额外的一个数组来维护每个集合的大小；而在合并的时候，会首先判断两颗树的大小，然后按照上面的思想进行合并，我们称树大小的值为加权，这种 union 算法称为加权 Quick-Union 算法

加权 Quick-Union 算法展开目录

class UF {
    private int[] id;
    private int[] sz;
    private int count;
    public UF(int N) {
        count = N;
        id = new int[N];
        sz = new int[N];
        for(int i = 0;i < N;i++) {
            id[i] = i;
            sz[i] = 1;
        }
    }
    public int count() {
        return count;
    }
    public boolean connected(int p,int q) {
        return find(p) == find(q);
    }
    public int find(int p) {
        while(p != id[p])
            p = id[p];
        return p;
    }
    public void union(int p,int q) {
        int pRoot = id[p];
        int qRoot = id[q];
        if(pRoot == qRoot)
            return;
        if(sz[pRoot] < sz[qRoot]) {
            id[pRoot] = qRoot;
            sz[qRoot] += sz[pRoot];
        } else {
            id[qRoot] = pRoot;
            sz[pRoot] += sz[qRoot];
        }
        count--;
    }
}

可以发现，通过 sz 数组决定如何对两棵树进行合并之后，最后得到的树的高度大幅度减小了。这是十分有意义的，因为在 Quick-Union 算法中的任何操作，都不可避免的需要调用 find 方法，而该方法的执行效率依赖于树的高度。树的高度减小了，find 方法的效率就增加了，从而也就增加了整个 Quick-Union 算法的效率。

上图其实还可以给我们一些启示，即对于 Quick-Union 算法而言，节点组织的理想情况应该是一颗十分扁平的树，所有的孩子节点应该都在 height 为 1 的地方，即所有的孩子都直接连接到根节点。这样的组织结构能够保证 find 操作的最高效率。那么如何构造这种理想结构呢？

在 find 方法的执行过程中，不是需要进行一个 while 循环找到根节点嘛？如果保存所有路过的中间节点到一个数组中，然后在 while 循环结束之后，将这些中间节点的父节点指向根节点，不就行了么？但是这个方法也有问题，因为 find 操作的频繁性，会造成频繁生成中间节点数组，相应的分配销毁的时间自然就上升了。那么有没有更好的方法呢？还是有的，即将节点的父节点指向该节点的爷爷节点，这一点很巧妙，十分方便且有效，相当于在寻找根节点的同时，对路径进行了压缩，使整个树结构扁平化。相应的实现如下，实际上只需要添加一行代码：

public int find(int p) {
    while(p != id[p]) {
        id[p] = id[id[p]];
        p = id[p];
    }
    return p;
}

至此，并查集算法基本上就介绍完了，从容易想到的 Quick-Find 到相对复杂但是更加高效的 Quick-Union，然后到对 Quick-Union 的几项改进，让我们的算法的效率不断的提高。

这几种算法的时间复杂度如下所示：
如果需要的功能不仅是检测两个节点是否连通，还需要在连通时得到具体的路径，那么就需要别的算法了，比如 DFS 或 BFS。