2017百度之星初赛（A）

题目链接：HDOJ6108

思路

假设P进制下有个数$(abc)_P$，若这个数满足：$(abc)_P \% B = 0$，则以下两个等式一定成立：

1. $(a*P^2 + b *P^1 + c *P^0) \% B = sum \% B = 0$
2. $(a + b + c) \% B = ans \% B = 0$

以上两个式子同时成立的条件是：P % B = 1，所以满足条件的B的个数为P - 1的因子数

代码

import java.util.*;
public class Main {
    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        int T = cin.nextInt();
        while((T--) != 0) {
            int n = cin.nextInt();
            solve(n - 1);
        }
    }
    private static void solve(int x) {
        int ans = 2;
        for(int i = 2;i <= Math.sqrt(x);i++) 
            if(x % i == 0)
                ans += 2;
        if((int)Math.sqrt(x) * (int)Math.sqrt(x) == x) 
            ans--;
        System.out.println(ans);
    }
}

每个数至少两个因子，一个1，一个本身，所以初始化ans=2，其次，只用遍历到$\sqrt{x}$即可，找到可以除尽的ans就加2，因为每个数的因子都是成对的，最后如果这个数本身就是个完全平方数，那就再减掉一个即可

题目链接：HDOJ6112

思路

基姆拉尔森公式的应用，注意一下2月29号的情况

代码

import java.util.Scanner;
public class Main {
    public static int day(int y,int m,int d) {
        if(m == 1 || m == 2) {
            m += 12;
            y -= 1;
        }
        int w=(d + 2*m + 3*(m + 1)/5 + y + y/4 - y/100 + y/400+ 1) % 7;
        return w;
    }
    public static boolean runnian(int a) {
        if((a % 4 == 0 && a % 100 != 0) || a % 400 == 0)
            return true;
        return false;
    }
    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        int t,y,m,d;
        t = cin.nextInt();
        while((t--) != 0) {
            String str = cin.next();//录入字符串
            String[] strs = str.split("-");//使用正则表达式进行分割
            y = Integer.parseInt(strs[0]);
            m = Integer.parseInt(strs[1]);
            d = Integer.parseInt(strs[2]);
            boolean flag = false;
            if(m == 2 && d == 29)
                if(runnian(y))
                    flag = true;
            int x = day(y,m,d);
            for(int i = y + 1;i <= 10000;i++) {
                if(flag) {
                    if(day(i,m,d) == x && runnian(i)) {
                        System.out.println(i);
                        break;
                    }
                } else {
                    if(day(i,m,d) == x) {
                        System.out.println(i);
                        break;
                    }
                }
            }
        }
    }
}

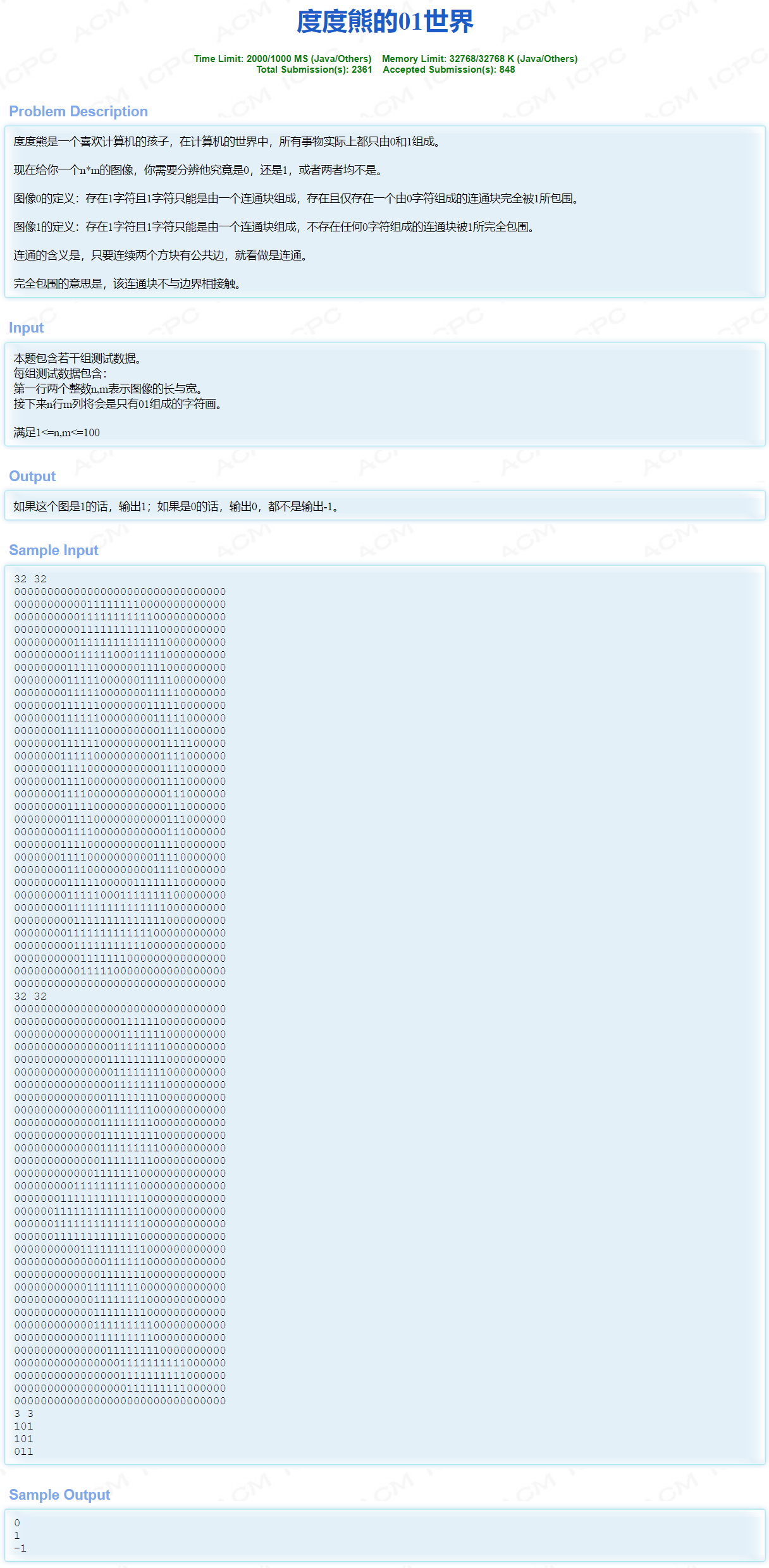
题目链接：HDOJ6113

思路

dfs,先深搜一遍看看1是不是只组成了1个连通块。然后搜一遍所有0组成的连通块，如果它碰到了地图的边界，那么它就不被1所完全包含，否则它被1组成的连通块完全包含。最后看看有几个被1包含的0组成的连通块即可，还要注意一下没有1的情况

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 105;
const int dr[4][2] = {{-1,0},{1,0},{0,-1},{0,1}};
bool f[maxn][maxn];
bool vis[maxn][maxn];
char s[maxn];
int n,m,num;
bool check(int x,int y,int z) {
    if(x >= 1 && y >= 1 && x <= n && y <= m && f[x][y] == z && !vis[x][y])
        return true;
    return false;
} 
bool dfs(int x,int y,int z) {
    bool flag = true;
    if(x == 1 || x == n || y == 1 || y == m)
        flag = false;
    if(f[x][y])
        num--;
    vis[x][y] = true;
    for(int i = 0;i <= 3;i++) {
        int dx = x + dr[i][0];
        int dy = y + dr[i][1];
        if(check(dx,dy,z))
            flag &= dfs(dx,dy,z);
    }
    return flag;
}
int main() {
    ios::sync_with_stdio(false);
    while(cin >> n >> m) {
        num = 0;
        for(int i = 1;i <= n;i++) {
            cin >> s;
            for(int j = 1;j <= m;j++) {
                f[i][j] = s[j - 1] - '0';
                if(f[i][j])
                    num++;
            }
        }
        memset(vis,false,sizeof(vis));
        int yy = 0;
        for(int i = 1;i <= n;i++) {
            for(int j = 1;j <= m;j++) {
                if(!vis[i][j] && f[i][j]) {
                    dfs(i,j,1);
                    yy++;
                }    
            }
        }
        if(yy != 1) 
            cout << -1 << endl;
        else {
            int x = 0;
            for(int i = 1;i <= n;i++) {
                for(int j = 1;j <= m;j++) {
                    if(!vis[i][j]) {
                        bool k = dfs(i,j,0);
                        if(k)
                            x++;
                    }
                }
            }
            if(!x)
                cout << 1 << endl;
            else {
                if(x == 1)
                    cout << 0 << endl;
                else 
                    cout << -1 << endl;
            }
        }
    }
}