LeetCode329. 矩阵中的最长递增路径

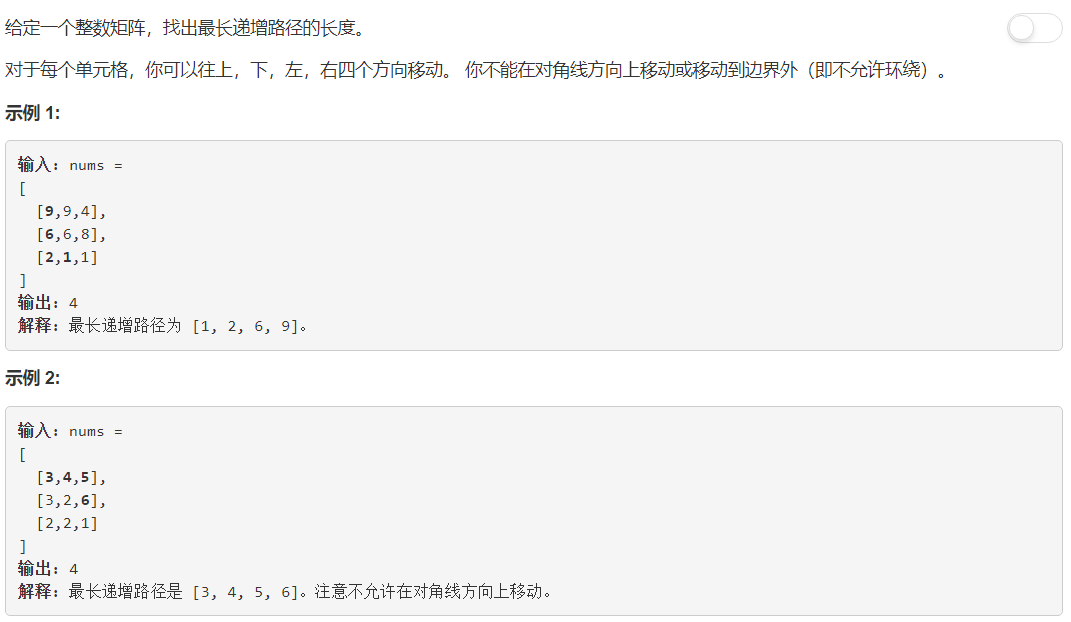
dfs，主函数中枚举起点，然后 dfs 函数中枚举四个方向进行移动，但是光 dfs 还不够，因为我们发现存在很多冗余，所以这是一道 dfs+dp 的问题，resulti 表示以 i,j 为终点的最长递增路径的长度

class Solution {
    public int n,m;
    public int[][] dr = {{-1,0},{1,0},{0,-1},{0,1}};
    public int[][] result = new int[1000][1000];
    public boolean check(int x,int y,int nx,int ny,int[][] matrix) {
        return nx >= 0 && ny >= 0 && nx < n && ny < m && matrix[nx][ny] > matrix[x][y];
    }
    public int dfs(int x,int y,int[][] matrix) {
        int max = 0;
        if(result[x][y] != 1)
            return result[x][y];
        for(int i = 0;i < 4;i++) {
            int nx = x + dr[i][0];
            int ny = y + dr[i][1];
            if(check(x,y,nx,ny,matrix))
                result[x][y] = Math.max(result[x][y],dfs(nx,ny,matrix) + 1);
        }
        return result[x][y];
    }
    public int longestIncreasingPath(int[][] matrix) {
        n = matrix.length;
        if(n == 0)
            return 0;
        m = matrix[0].length;
        int ans = 0;
        for(int i = 0;i < 1000;i++) 
            for(int j = 0;j < 1000;j++) 
                result[i][j] = 1;
        for(int i = 0;i < n;i++) {
            for(int j = 0;j < m;j++) {
                ans = Math.max(ans,dfs(i,j,matrix));
            }
        }
        return ans;
    }
}