TRIE（2）

实现 TRIE 结构展开目录

第一种方法是用一个二维数组来存储：

int trie[MAX_NODE][CHARSET];
int k;

其中 MAX_NODE 是 trie 中最大能存储的节点数目，CHARSET 是字符集的大小，k 是当前 trie 中包含有多少个节点。Trie [i][j] 的值是 0 表示 trie 树中 i 号节点，并没有一条连出去的边，满足边上的字符标识是字符集中第 j 个字符（从 0 开始）；trie [i][j] 的值是正整数 x 表示 trie 树中 i 号节点，有一条连出去的边，满足边上的字符标识是字符集中第 j 个字符，并且这条边的终点是 x 号节点

举个例子，下图中左边是 trie 树，右边是二维数组 trie 中非 0 的值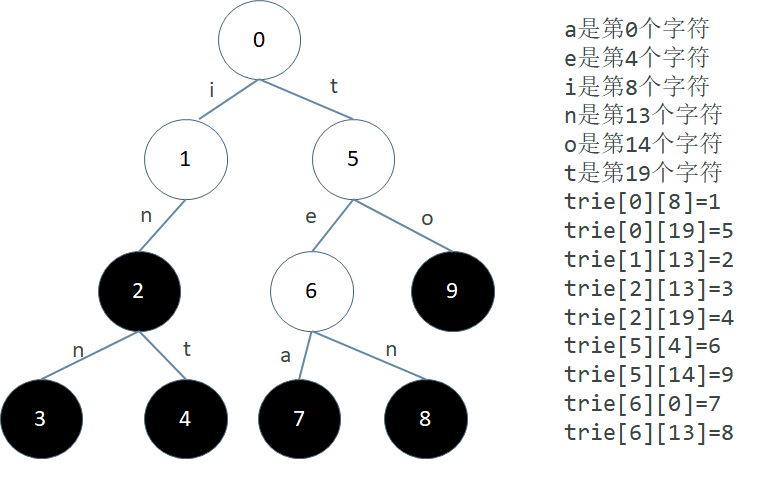
用二维数组实现 trie 的好处是用起来非常方便，因为 trie 的 insert 和 search 操作都要经常判断一个节点有没有标识某个字符的边，以及边的终点是几号节点。用二维数组的话，我们只要看相应的 trie [i][j] 的值即可。用二维数组的缺点是可能会浪费很多空间，因为我们对每一个节点都用了一个字符集大小的数组存储子节点号，但实际上每个点连出去的边很稀疏。比如上图中实际上每个点只有 0-2 个子节点，但是我们给每个节点都开辟了一个大小是 26 的数组去存储子节点

第二种方法是像邻接表一样用 vector 来存储每个节点的子节点：

vector<pair<char, int> > trie[MAX_NODE];
int k;

我们把 i 号节点的子节点和边的信息存在 trie [i] 里。每一个 pair<char, int > 其实是（边的标识，子节点号）这样的二元组：

用 vector 的好处是可以节省很多空间，起码理论上空间复杂度是 O (N) 的，其中 N 是节点总数。缺点是每次我们想找 i 号节点有没有标识是某个字符 ch 的边时，都需要遍历一遍 trie [i] 这个 vector，而不能像数组一样直接查找

第三种方法是用 unordered_map

unordered_map<char, int> trie[MAX_NODE];
int k;

使用 unordered_map 看上去是一个两全其美的做法。每次我们想找 i 号节点有没有标识是某个字符 ch 的边时，只要看 trie [i][ch] 的值即可。同时理论上也不需要每个节点都占用 CHARSERT 大小的空间去存储子节点，而是有几个子节点就用到几个子节点的空间。理论上时空复杂度都是 O (N)

我们采用数组的方式来存储，下面分别看一下 insert 和 search 方法

#include <iostream>
#include <cstring>
using namespace std;
const int MAX_NODE = 1000000 + 10;
const int CHARSET = 26;
int trie[MAX_NODE][CHARSET] = {0};
int color[MAX_NODE0] = {0};
int k = 1;
void insert(char *w) {
    int len = strlen(w);
    int p = 0;
    for(int i = 0;i < len;i++) {
        int c = w[i] - 'a';
        if(!trie[p][c]) {
            trie[p][c] = k;
            k++;
        }
        p = trie[p][c];
    }
    color[p] = 1;
}

代码的第 6~8 行，一开始 trie [][] 被初始化为 0，保证每个节点被创建出来时，都没有子节点。K 初始化为 1 表示一开始只有 1 个节点，也就是 0 号节点根节点。Color 是用来标记一个节点是不是终结点。Color [i]=1 标识 i 号节点是终结点

第 9~21 行是插入函数 insert (w)，w 是字符指针，实际上可以看作是一个字符串

第 11 行是 p 从 0 号节点开始。第 12~19 行是依次插入 w 的每一个字符。第 13 行是计算 w [i] 是字符集第几个字符，这里我们假设字符集只包含 26 个小写字母。第 14~17 行是如果 p 没有连出标识是 w [i] 的边，那么就创建一个。这里新创建的节点一定就是 k 号节点。所谓创建新节点实际上也没什么可创建的，新节点就是个编号。所以我们直接令 triei=k 即可，然后将 k 累加 1，整个创建过程就完成了。第 18 行是沿着标记着 w [i] 的边移动到下一个节点。最后第 20 行，是将最后到达的节点 p 标记为终结点

有了插入，我们再看查找代码如何实现：

int search(char *s) {
    int len = strlen(s);
    int p = 0;
    for(int i = 0;i < len;i++) {
        int c = s[i] - 'a';
        if(!trie[p][c]) return 0;
        p = trie[p][c];
    }
    return color[p] == 1;
}

查找的代码就比较简单直观，search 返回 0 表示 trie 中没有 s，返回 1 表示有 s。第 3 行是从 p=0 也就是根节点开始。第 4~8 行是枚举 s 的每一个字符。第 5 行是计算当前字符 s [i] 在字符集的序号。第 6 行是判断 p 节点有没有连出标识 s [i] 字符的边，如果没有，说明现在无路可走，直接返回 0；如果有的话，第 7 行就是移动到下一个节点。如果整个循环结束还没有 return 0，那就说明成功沿着 s 的每一个字符到达了 p 节点。这时只要判断 p 节点是不是终结点即可，也就是第 9 行的代码

例 1 题目链接：hihoCoder1014展开目录

这道题目的大意是给定一个包含 N 个字符串的集合，然后再给出 M 个询问。每次询问给出一个字符串 s，要求你回答集合中有几个字符串的前缀是 s

比如集合是 {babaab， babbbaaaa， abba， aaaaabaa， babaabab} 询问前缀是 bab，答案就是 3。因为有 babaab， babbbaaaa， babaabab 三个字符串前缀是 bab

这道题是一道很经典的用 Trie 解决的题目。首先我们把集合中的 N 个字符串都插入到 trie 中。对于每一个查询 s 我们在 trie 中查找 s，如果查找过程中无路可走，那么一定没有以 s 为前缀的字符串。如果最后停在一个节点 p，那我们就要看看以 p 为根的子树里一共有多少终结点。终结点的数目就是答案

比如在上图中，询问是 s=”in”。我们会停在 2 号节点上。这棵子树一共有 3 个终结点，对应着 3 个字符串”in”, “inn”, “int”，这三个字符串前缀都是”in”，所以答案是 3

但是如果我们每次都遍历以 P 为根的子树，那时间复杂度就太高了。解决的办法是用空间换时间，我们增加一个数组 int cnt [MAX_NODE]，cnt [i] 记录的是以 i 号节点为根的子树中，有几个终结点。然后我们每次 insert 一个字符串的时候，顺便就把沿途的节点的 cnt 值都 + 1。这样就不用每次遍历以 P 为根的子树，而是直接输出 cnt [P] 即可

#include <iostream>
#include <cstring>
using namespace std;
const int MAX_NODE = 1000000 + 10;
const int CHARSET = 26;
int trie[MAX_NODE][CHARSET] = {0};
int cnt[MAX_NODE] = {0};
int n,m,k = 1;
char s[20];
void insert(char *w) {
    int len = strlen(w);
    int p = 0;
    for(int i = 0;i < len;i++) {
        int c = w[i] - 'a';
        if(!trie[p][c]) {
            trie[p][c] = k;
            k++;
        }
        p = trie[p][c];
        cnt[p]++;
    }
}
int search(char *s) {
    int len = strlen(s);
    int p = 0;
    for(int i = 0;i < len;i++) {
        int c = s[i] - 'a';
        if(!trie[p][c]) return 0;
        p = trie[p][c];
    }
    return cnt[p];
}
int main() {
    memset(trie,0,sizeof(trie));
    scanf("%d",&n);
    for(int i = 0;i < n;i++) {
        scanf("%s",s);
        insert(s);
    }
    scanf("%d",&m);
    while(m--) {
        scanf("%s",s);
        int ans = search(s);
        printf("%d\n",ans);
    }
    return 0;
}