Trie又被称为前缀树或者字典树。它的基本作用是用来存储一个字符串集合:{W1, W2, W3, … WN},并且可以用来查询一个字符串S是不是在集合里。具体来说,Trie一般支持两个操作:
- Trie.insert(W):第一个操作是插入操作,就是将一个字符串W加入到集合中
- Trie.search(S):第二个操作是查询操作,就是查询一个字符串S是不是在集合中
由于Trie的特性,它还特别适合处理一些与前缀有关的查询,比如集合中有几个字符串与S有公共前缀这样的查询。首先我们来看一下Trie长什么样子:
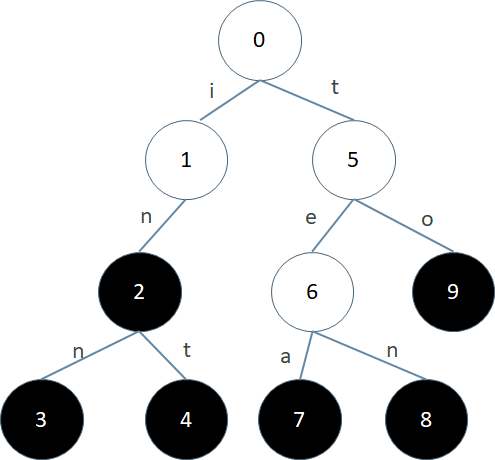
上面这棵Trie树包含的字符串集合是{in, inn, int, tea, ten, to}。每个节点的编号是我们为了描述方便加上去的。树中的每一条边上都标识有一个字符。这些字符可以是任意一个字符集中的字符。比如对于都是小写字母的字符串,字符集就是’a’-‘z’;对于都是数字的字符串,字符集就是’0’-‘9’;对于二进制字符串,字符集就是0和1
从一个节点连出去的边都必须标识不同的字符。所以一个节点最多有|字符集|这么多子节点。其中有一些节点是终结点,我们用黑色表示。对于每一个终结点,如果我们把从根到它的路径上的字符按顺序连起来,就对应着一个集合中的字符串
比如上图中3号节点对应的路径0123上的字符串是inn,8号节点对应的路径0568上的字符串是ten。终结点与集合中的字符串是一一对应的
TRIE插入
那么对于给定的字符串集合{W1, W2, W3, … WN}如何创建对应的Trie树呢?其实Trie树的创建从根节点开始,通过依次将W1, W2, W3, … WN插入Trie中实现。所以关键就是之前提到的Trie的插入操作
假设我们要插入字符串"in"。我们一开始位于根,也就是0号节点,我们用P=0表示。我们先看P是不是有一条标识着i的连向子节点的边。没有这条边,于是我们就新建一个节点,也就是1号节点,然后把1号节点设置为P也就是0号节点的子节点,并且将边标识为i。最后我们移动到1号节点,也就是令P=1
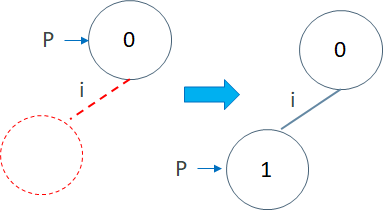
这样我们就把”in”的"i"字符插入到Trie中了。然后我们再插入字符"n",先找P也就是1号节点有没有标记为n的边。还是没有,于是再新建一个节点2,设置为P也就是1号节点的子节点,并且把边标识为n。最后再移动到P=2。这样我们就把n也插入了。由于n是"in"的最后一个字符,所以我们还需要将P=2这个节点标记为终结点

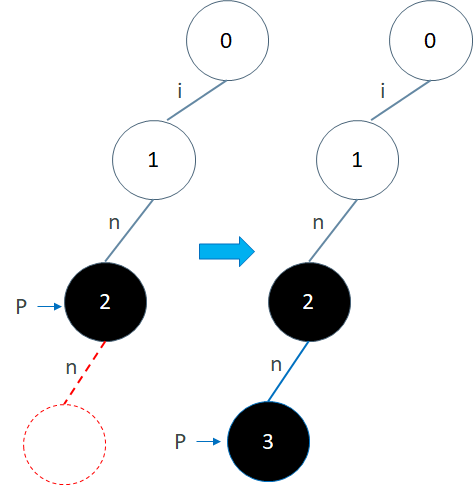
现在我们再插入字符串"inn"。过程也是一样的,从P=0开始找标识为i的边,这次找到1号节点。于是我们就不用创建新节点了,直接移动到1号节点,也就是令P=1。再插入字符n,也是有2号节点存在,所以移动到2号节点,P=2。最后再插入字符n这时P没有标识为n的边了,所以新建3号节点作为2号节点的子节点,边标识为n,同时将3号节点标记为终结点
综上所述,在Trie中插入一个字符串W的伪代码如下:
Insert(W):
P = root
For i = 1...W.len
If P.thru(W[i]) == NULL//没有标识为W[i]的边
P.addChild(W[i],new Node())
P = p.thru(W[i])
P.markEndPoint()//标记P为终结点TRIE查找
查找其实比较简单。只要从根节点开始,沿着标识着S[1] -> S[2] -> S[3] … -> S[S.len]的边移动,如果最后成功到达一个终结点,就说明S在Trie树中;如果最后无路可走,或者到达一个不是终结点的节点,就说明S不在Trie树中
比如上图中查找"inn",就会从0号节点经过1号节点和2号节点,最后到达3号节点。3号节点是终结点,所以inn在Trie树中。再比如查找"ten",就会从0号节点,经过56到达8号节点。8号节点也是终结点,所以ten也在Trie树中
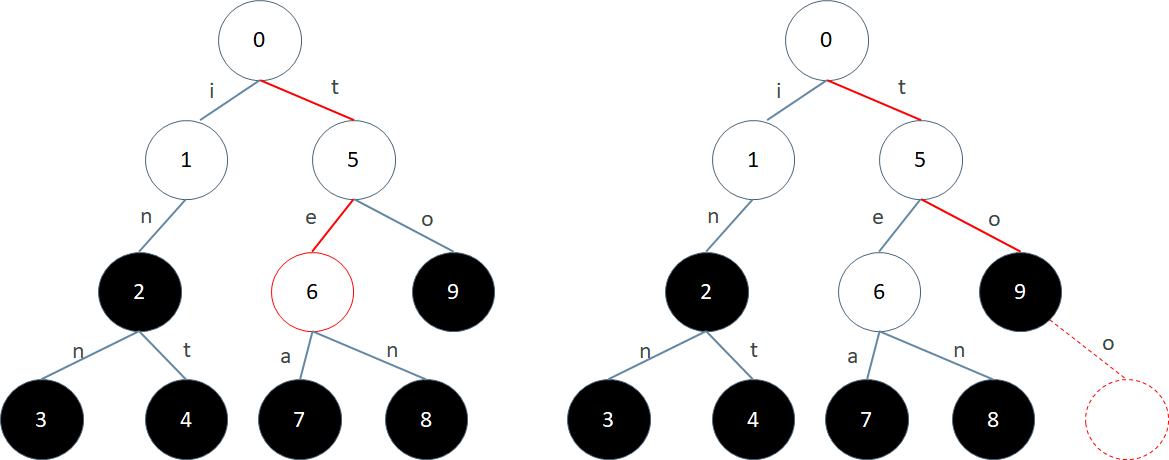
如果是查找"te",就会从0开始经过5最后到达6。但是6不是终结点,所以te没在Trie树中。如果查找的是"too",就会从0开始经过5和9,然后发现之后无路可走:9号节点没有标记为o的边连出去。所以too也不在Trie中
综上所述,在Trie树中查找一个字符串的伪代码如下:
Search(S):
P = root
For i = 1...S.len
If P.thru(S[i]) == NULL
Return FALSE
P = P.thru(S[i])
Return TRUE需要注意一点,由字符串集合{W1, W2, W3, … WN}创建的Trie中包含的节点数最多有W1.len+W2.len+W3.len+…+WN.len这么多。当然有可能因为一些字符串有相同的前缀,减少一些节点,不过最坏情况我们还是要做到心中有数
