例6 题目链接：POJ2752
这道题目的大意是给定一个字符串S，让找出所有既是S前缀又是S后缀的字符串。然后从小到大输出它们的长度
比如S=ababcababababcabab，既是前缀又是后缀的有ab, abab, ababcabab和S本身。所以输出的是2 4 9 18。再比如S=aaaaa，既是前缀又是后缀的有a, aa, aaa, aaaa和S本身。所以输出的是1 2 3 4 5
next数组的定义是：如果P[1..k]是P[1..j]的最长的满足“既是前缀也是后缀”的字符串，那么next[j]=k。并且P[1..j]的所有满足“既是前缀也是后缀”的字符串都通过next数组的连线连在一起。比如满足既是babab前缀又是babab后缀的字符串有bab和b，对应next[5]=3和next[3]=1
所以这道题的解法就是把输入的字符串当作P，求出P的next数组，则{m, next[m], next[next[m]], … }反转一下顺序就是答案
#include <iostream>
#include <cstring>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
int nxt[1000001];
int m,t;
char p[1000001];
vector<int> ans;
int main()
{
while(scanf("%s",p + 1) != EOF)
{
ans.clear();
m = strlen(p + 1);
nxt[0] = -1;
int j = -1;
for(int i = 1;i <= m;i++)
{
while(j >= 0 && p[j + 1] != p[i])
j = nxt[j];
nxt[i] = ++j;
}
while(m)
{
ans.push_back(m);
m = nxt[m];
}
reverse(ans.begin(),ans.end());
for(int i = 0;i < ans.size();i++)
{
cout << ans[i];
if(i == ans.size() - 1)
cout << endl;
else
cout << " ";
}
}
return 0;
}例7 题目链接：POJ2406
这道题的大意是：对于一个字符串S，我们把S重复K次得到的字符串记作S^K。比如(ab)^3=ababab，(abc)^2=abcabc， abcd^1=abcd。现在给定一个字符串S，让你求出最大的整数K，使得S能表示成一个字符串的K次方
例如对于S=abcd，就只能表示成abcd^1；S=aaaa就能表示成a^4；S=ababab就能表示成ab^3
这类同字符串循环节有关的题目是next数组的经典应用场景。首先我们来看一个定理：字符串P是由t个字符循环K次组成的，当且仅当P.len = t * K且P[1..P.len-t]是P的后缀。我们看一下下图中的几个例子应该就比较清楚了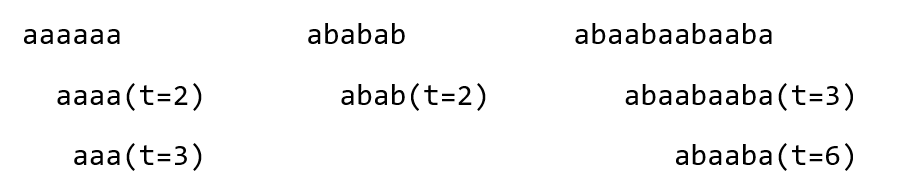
需要注意的是，如果只有 “P[1..P.len-t]是P的后缀“这一个条件，P不一定是t个字符循环的。例如”abcdab“是”abcdabcdab”的后缀，但是”abcdabcdab”并不是t=4个字符循环的
有了这个定理，我们再求解上面的问题就简单多了。对于输入的字符串P，假设P的长度是m。我们知道满足P[1..j]是P的后缀的整数j，都在next[m], next[next[m]]……这条链上。所以我们可以依次遍历这条链上的每一个整数x，再判断m-x是不是m约数，这里m-x就是循环节长度t。最后找一个m-x是m约数的最大的x，m/(m-x)即是答案
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
int nxt[1000001];
int m,x,ans;
char p[1000001];
int main()
{
scanf("%s",p + 1);
while(strcmp(p + 1,".") != 0)
{
m = strlen(p + 1);
nxt[0] = -1;
int j = -1;
for(int i = 1;i <= m;i++)
{
while(j >= 0 && p[j + 1] != p[i])
j = nxt[j];
nxt[i] = ++j;
}
x = nxt[m];
while(x != -1)
{
if(m % (m - x) == 0)
{
ans = m - x;
break;
}
x = nxt[x];
}
cout << m / ans << endl;
scanf("%s",p + 1);
}
return 0;
}例8 题目链接：HUSTOJ1010
这道题的大意就是给定一个字符串S，让你找到S的最短的循环节。这里循环次数可以不是整数，例如abcd循环2.25次是abcdabcda，bca循环2(1/3)是bcabcab，efgacbd循环2(1/7)是efgabcdefgabcde
这道题和之前一题很类似，区别就是允许最后一段是残缺的，可以不是完整的循环。之前那道题我们有个定理：字符串P是由t个字符循环K次组成的，当且仅当P.len = t * K且P[1..P.len-t]是P的后缀。这道题不要求完整循环K次，其实等价于不需要P.len是t的倍数。所以我们求出next数组之后，m-next[m]就是答案
例9 题目链接：POJ2185
这道题的大意是给一个R*C的二维字符矩阵A，然后让你找到一个面积最小的二维矩阵B，满足B循环铺开若干次之后就能得到A
注意本题中循环铺开也不需要完整循环。例如
ABABA
ABABA
就可以看作是AB在X方向上循环了2.5次，在Y方向上循环了2次得到的
这道题也是找循环节，允许循环不完整。但是与之前的题目最大的区别是这道题是二维的。解决这道题的关键是意识到二维矩阵的循环实际上在2个维度上是独立的，可以分别计算
比如我们先处理X方向上的循环节，就可以把矩阵的每一列看成一个“字符“，只不过这个”字符“实际上是一个字符R元组。这样整个矩阵就可以看成是包含C个”字符“的”字符串“。然后我们求这个”字符串“的循环节就可以得到X方向的循环节长度。当然在这种情况下，比较两个”字符“相等的方法是比较两个R元组是不是完全相等
对于Y方向的循环节也可以用类似的方法：把一行C元组看成一个“字符“，然后在R个”字符“的字符串上找循环节。最后两维的循环节长度相乘就是答案
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
int nxt[1000001];
int n,m,x,ans;
char p[10001][80];
bool samec(int i,int j)
{
for(int k = 1;k <= n;k++)
if(p[k][i] != p[k][j])
return false;
return true;
}
bool samer(int i,int j)
{
for(int k = 1;k <= m;k++)
if(p[i][k] != p[j][k])
return false;
return true;
}
int main()
{
std::ios::sync_with_stdio(false);
scanf("%d%d",&n,&m);
for(int i = 1;i <= n;i++)
scanf("%s",&p[i][1]);
nxt[0] = -1;
int j = -1;
for(int i = 1;i <= m;i++)
{
while(j >= 0 && !samec(j + 1,i))
j = nxt[j];
nxt[i] = ++j;
}
ans = m - nxt[m];
j = -1;
for(int i = 1;i <= n;i++)
{
while(j >= 0 && !samer(j + 1,i))
j = nxt[j];
nxt[i] = ++j;
}
ans *= n - nxt[n];
cout << ans << endl;
return 0;
}上面代码第28~35是在求X方向的循环节，第37~43是在求Y方向的循环节。最后(m-nxt[m])*(n-nxt[n])就是答案。注意第32行和40行，原本在求next数组的比较是p[j+1] != p[i]，因为这里要比较的是R元组或C元组，所以我们用了!samec(j+1, i)和!samer(j+1, i)进行比较
