$\mathcal {Y}$-Tuning: 通过对标签表征进行微调的深度学习新范式

ACL2022 有一篇名为《$\mathcal{Y}$-Tuning: An Efficient Tuning Paradigm for Large-Scale Pre-Trained Models via Label Representation Learning》的投稿，从标题上就吸引了我的注意，不同于 Fine-Tuning、Adapter-Tuning、Prompt-Tuning，这篇文章的创新之处在于，不调整输入文本特征与大规模预训练模型的参数，仅通过学习标签的特征，以往很少见到论文去学习标签的特征。虽然最终效果可能仍无法与微调相比，但它在节省计算成本方面有很大的优势，并有可能通过后续研究进一步提高性能

Preliminaries of Tuning PTMs

对于 NLP 任务来说，通常都含有输入文本 $x\in \mathcal {X}$ 以及标签 $y\in \mathcal {Y}$，其中 $\mathcal {X}$ 的特征空间是离散的（例如 One-hot）。以情感分析（Sentiment Analysis, SA）任务为例，输入句子

$$ x = \text{I love this movie} $$

标签集 $\mathcal {Y}=\{\text {postive}, \text {negative}\}$ 中的标签 $y=\text {postive}$ 为真实标签

定义 $\phi : \mathcal {X}\to \mathcal {Z}$ 为输入句子到高维稠密向量空间的映射，$f: \mathcal {Z}\to \mathcal {Y}$ 为该向量空间到标签空间的映射。给定训练集 $\mathcal {D}$，我们可以定义损失函数为 $\ell: \mathcal {Y}\times \mathcal {Y}\to \mathbb {R}^+$，并且可以通过以下方法找到最佳的 $f$ 和 $\phi$：

$$ \phi, f = \mathop{\arg \min} \sum_{(x,y)\in \mathcal{D}} \ell (f(\phi (x)), y)\tag{1} $$

通常来说，即便分类器 $f$ 很简单，但只要有一个好的特征提取器 $\phi (x)$，下游任务中的表现就不会差

上面的内容删减自原论文，论文中的描述有些抽象，说白了实际上 $\phi$ 可以看作是 BERT，$f$ 就是为了满足不同的下游任务，而接在 BERT 后面的一些层，例如文本分类后面接的就是一个 Linear 层

$\mathcal{Y}$-Tuning

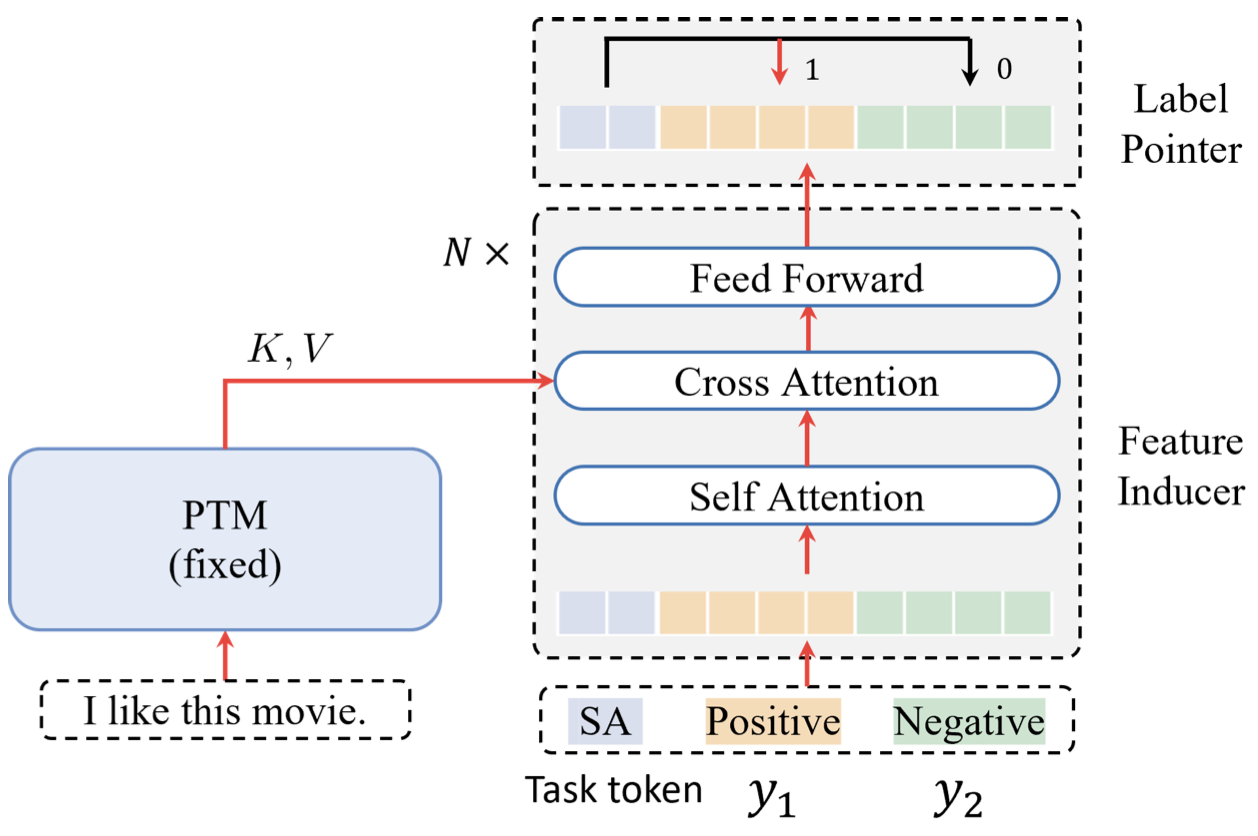
我们定义 $(x,y)$ 是一个有标签的训练样本，$\phi^{\star}$ 是在大规模语料上训练好的预训练模型，并且在接下来始终固定 $\phi^{\star}$ 的参数不更新。传统做法是微调特征提取器 $\phi^{\star}$ 的参数，使其接近真实标签。$\mathcal {Y}$-Tuning 的做法是固定 $\phi^{\star}$ 的参数，转而微调标签提取器 $\psi$ 的参数，并且我们使用 Cross Attention 将 $\phi^{\star}(x)$ 与 $\psi (\mathcal {Y})$ 的特征进行融合，如下图所示

PTMs 代表 φ

损失函数为 Triplet Loss，形式如下：

$$ \begin{aligned} \mathcal{L}_{\psi,f}(x,y) = &\sum_{y' \in \mathcal{Y}\atop y'\neq y}[f(\phi^{\star}(x), \psi(y^{\prime}))\\ &-f(\phi^{\star}(x), \psi(y)) + \alpha]_{+} \end{aligned}\tag{2} $$

其中，$[x]_+=\max (x, 0)$，$\alpha$ 是一个边界超参数，用于控制正负样本间的距离。在训练过程中，给定训练集 $\mathcal {D}$，我们可以通过如下方式找到最佳的模型参数

$$ \psi, f = \arg \min \sum_{(x,y)\in \mathcal{D}} \mathcal{L}_{\psi, f}(x,y)\tag{3} $$

在推理阶段，我们可以使用如下方式获得预测值：

$$ \hat{y} = \mathop{\arg \max}_{y\in \mathcal{Y}}\ f(\phi^{\star}(x), \psi(y))\tag{4} $$

An Implementation of $\mathcal{Y}$-Tuning

论文图中的模型架构主要由三个部分组成：

1. 用于提取文本特征的 $\phi$，这个部分一般是 Encoder 类模型，例如 BERT 等
2. 用于提取标签特征的 $\psi$，这个部分一般采用 Transformer 的 Decoder 结构，因为需要有 Cross-Attention 的部分对标签特征和文本特征进行交互
3. 用于预测类别的标签指针（Label Pointer），这个部分比较简单，用一个平均或者最大池化将高维向量转为低维向量即可

Label Embedding

给定一个标签集 $\mathcal {Y}$，我们首先将标签 $y\in \mathcal {Y}$ 映射为一个或多个连续的向量。当然，除了标签外，我们还需要将任务相关的信息映射为向量，例如情感分析任务，我们会在最前面添加一个 SA 标志

这其实有点像 mBART，在做机器翻译的时候将该语言对应的标志（例如 ZH、JP、EN 等）添加到句子前面

因此，初始的标签特征为

$$ \mathbf{Y} = [e_T; e_1^{(1)};···;e_1^{(c)}] \in \mathbb{R}^{N\times D}\tag{5} $$

其中，$e_T$ 表示任务相关的 embedding，$e^{(c)}$ 表示第 $c$ 个类别的 embedding，$N$ 和 $D$ 分别表示样本数量以及标签的表征的维度。实际上每个标签都可以用多个向量来表示，作者也做了一个对比实验，研究每个标签用多个向量来表示会对结果产生什么影响

有很多方法将标签 $y$ 映射为一个向量，例如从 Vocabulary、均匀分布、token embedding 中采样等

Self-Attention and Cross-Attention

我们首先使用 self-attenion 加强不同标签间的信息交互

$$ \text{Att}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{Softmax}\left(\frac{\mathbf{Q}\mathbf{K}^{\top}}{\sqrt{D_k}}\right)\mathbf{V}\tag{6} $$

其中，$\mathbf {Q}\in \mathbb {R}^{N\times D_k}, \mathbf {K}\in \mathbb {R}^{M\times D_k}, \mathbf {V}\in \mathbb {R}^{M\times D_v}$，如果在 self-attention 中，$N=M$；如果在 cross-attention 中，$N$ 代表输入句子的长度，$M$ 代表标签输入的长度

在 cross-attention 中

$$ \mathbf{Q}=\mathbf{Y}\mathbf{W}_q\in \mathbb{R}^{N\times D}\\ \mathbf{K}=\mathbf{X}\mathbf{W}_k\in \mathbb{R}^{M\times D}\\ \mathbf{V}=\mathbf{X}\mathbf{W}_v\in \mathbb{R}^{M\times D} $$

其中，$\mathbf {X}$ 是输入句子通过 PTMs 后的高维向量

Label Pointer

所有计算完成之后，我们会得到输出向量

$$ \mathbf{h} = [\mathbf{h}_T, \mathbf{h}_1, ···,\mathbf{h}_C]\tag{7} $$

其中，$\mathbf {h}_T$ 是任务相关的描述特征，$\mathbf {h}_c$ 是类别为 $c$ 的标签特征。Triplet Loss 的定义如下：

$$ \mathcal{L}(x,y) = \sum_{c=1}^C [\mathbf{h}_T^{\top}\mathbf{h}_c - \mathbf{h}_{T}^{\top}\mathbf{h}_{c^{\star}} + \alpha]_{+}\tag{8} $$

其中，$c^{\star}$ 代表正确标签对应的索引

Model Analysis

假设我们有一个 $L$ 层的预训练模型，它的复杂度为 $\mathcal {O}(LM^2)$，其中 $M$ 是输入句子长度；一个有着长度为 $P$ 的连续型 Prompt，它的复杂度为 $\mathcal {O}(L (M+P)^2)$；对于 $\mathcal {Y}$-tuning 来说，self-attention 与 cross-attention 的复杂度分别为 $\mathcal {O}(N^2)$ 以及 $\mathcal {O}(MN)$，其中 $N$ 为标签集的大小。因为在 $\mathcal {Y}$-tuning 中我们是固定预训练模型参数不训练的，因此预训练模型的部分不会占用计算资源（尤其是反向传播过程）

Result

从实验结果上来看，效果算是「很有竞争力」，我们当然不能拿它与传统的 FineTune 相比，毕竟可训练的参数少了那么多，训练所需的算力也不是一个数量级的

个人总结

本文提出的 $\mathcal {Y}$-Tuning 思路非常有意思，传统思路是对输入句子进行学习，使其输出向量靠近标签的分布；而这篇文章正好相反，对标签进行学习。让我有些意外的点是，损失函数并不是传统的 CrossEntropyLoss，因为在我看来就直接将输出向量转换维度之后与真实标签进行对比就好了。但是论文使用的损失函数是 Triplet Loss，不知道为什么作者为什么要这样做