自《Attention is All You Need》一文发布后,基于Multi-Head Attention的Transformer模型开始流行起来,而BERT模型更是将Transformer模型的热度推上了又一个高峰。当然,技术的探索是无止境的,改进的工作也相继涌现:有改进预训练任务的,如XLNET的PLM、ALBERT的SOP等;有改进归一化的,如Post-Norm向Pre-Norm的改变,以及T5中去掉了Layer Norm里边的beta参数等;也有改进模型结构的,如Transformer-XL等;有改进训练方式的,如ALBERT的参数共享等;...
以上的这些改动,都是在Attention外部进行改动的,也就是说它们都默认了Attention的合理性,没有对Attention本身进行改动,而本文我们则介绍两个新的研究:它们针对Multi-Head Attention中可能存在的建模瓶颈,提出了不同的方案来改进Multi-Heaed Attention。两篇论文都来自Google,并且做了相当充分的实验,因此结果应该是相当具有说服力的
再小也不能小key_size
第一个结果来自文章《Low-Rank Bottleneck in Multi-head Attention Models》,它明确地指出了Multi-Head Attention里边的表达能力瓶颈,并提出通过增大key_size的方法来缓解这个瓶颈
Single-Head Attention
对一个单头注意力机制来说,它的定义如下:
$$ \text{Attention}(\boldsymbol{X})=\boldsymbol{W}_{v} \boldsymbol{X} \cdot \text{Softmax}\left[\frac{\left(\boldsymbol{W}_{k} \boldsymbol{X}\right)^{T}\left(\boldsymbol{W}_{q} \boldsymbol{X}\right)}{\sqrt{d_{k}}}\right]=\boldsymbol{W}_{v} \boldsymbol{X} \cdot \boldsymbol{P}\tag{1} $$
其中$\boldsymbol{W}_q\in \mathbb{R}^{d_q\times d},\boldsymbol{W}_k\in \mathbb{R}^{d_k\times d},\boldsymbol{W}_v\in \mathbb{R}^{d_v\times d}$,因为这是单头注意力机制,所以$d_q=d_k=d_v=d$
但是论文中提到如果$d_q=d_k=d\ge n$,那么给定列满秩矩阵$\boldsymbol{X}\in\mathbb{R}^{d\times n}$和$n\times n$的正随机矩阵(每一列的和为1,且矩阵所有元素都为正数)$\boldsymbol{P}$,一定存在$d\times d$维的$\boldsymbol{W}_q,\boldsymbol{W}_k$,使得
$$ \text{Softmax}\left[\frac{(\boldsymbol{W}_k\boldsymbol{X})^T(\boldsymbol{W}_q\boldsymbol{X})}{\sqrt{d_k}}\right]=\boldsymbol{P}\tag{2} $$
成立。但是如果$d<n$,则此公式不一定成立
首先证明$d\ge n$的情况。因为$\boldsymbol{X}$是列满秩矩阵,所以一定存在其左逆矩阵$\boldsymbol{X}^{\dagger}=(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\in\mathbb{R}^{n\times d}$,且$\boldsymbol{X}^{\dagger}\boldsymbol{X}=\boldsymbol{I}_n$,令$\boldsymbol{W}_k=\tilde{\boldsymbol{W}}_k\boldsymbol{X}^{\dagger},\boldsymbol{W}_q=\tilde{\boldsymbol{W}}_q\boldsymbol{X}^{\dagger}$,则
$$ \begin{aligned} (\boldsymbol{W}_k\boldsymbol{X})^T(\boldsymbol{W}_q\boldsymbol{X})=&\, \boldsymbol{X}^{T} \boldsymbol{W}_{k}^{T} \boldsymbol{W}_{q} \boldsymbol{X}\\ =&\, \boldsymbol{X}^{T}(\boldsymbol{X}^{\dagger})^{T} \tilde{\boldsymbol{W}}_{k}^{T} \tilde{\boldsymbol{W}}_{q} \boldsymbol{X}^{\dagger} \boldsymbol{X} \\ =&\, \boldsymbol{I}_{n} \cdot \tilde{\boldsymbol{W}}_{k}^{T} \tilde{\boldsymbol{W}}_{q} \cdot \boldsymbol{I}_{n} \\ =&\, \tilde{\boldsymbol{W}}_{k}^{T} \tilde{\boldsymbol{W}}_{q}\\\triangleq&\, \tilde{\boldsymbol{W}}_{k q} \end{aligned}\tag{3} $$
将式(3)的最终结果带入式(1)得
$$ \begin{aligned} \text{Softmax}\left[\frac{\left(\boldsymbol{W}_{k} \boldsymbol{X}\right)^{T}\left(\boldsymbol{W}_{q} \boldsymbol{X}\right)}{\sqrt{d_{k}}}\right]=&\, \text{Softmax}\left[\frac{\tilde{\boldsymbol{W}_{kq}}}{\sqrt{d_k}}\right]\\ =&\, \exp\left(\frac{\tilde{\boldsymbol{W}}_{kq}}{\sqrt{d_k}}\right)\cdot \boldsymbol{D}_{\tilde{\boldsymbol{W}}_{kq}}^{-1} \end{aligned}\tag{4} $$
其中$\boldsymbol{D}_{\tilde{\boldsymbol{W}}_{kq}}^{-1}$是一个$n\times n$的对角矩阵,并且
$$ \left(\boldsymbol{D}_{\tilde{\boldsymbol{W}}_{kq}}^{-1}\right)_{ii}=\sum_{j=1}^n \exp \left(\frac{\tilde{\left(\boldsymbol{W}_{kq}\right)_{ji}}}{\sqrt{d_k}}\right)=\left(\boldsymbol{1}^T\exp\left(\frac{\left(\tilde{\boldsymbol{W}}_{kq}\right)}{\sqrt{d_k}}\right)\right)_i\tag{5} $$
式(5)的$\boldsymbol{1}^T$是一个全1的行向量,其实很好理解,用一个全1的行向量右乘一个矩阵,本质就是求和操作
因此,我们现在转而需要证明下式成立
$$ \exp\left(\frac{\tilde{\boldsymbol{W}}_{kq}}{\sqrt{d_k}}\right)=\boldsymbol{P}\cdot \boldsymbol{D}_{\tilde{\boldsymbol{W}}_{kq}}\tag{6} $$
给定$\boldsymbol{P}$,为了构建矩阵$\tilde{\boldsymbol{W}}_{kq}$,我们随意选择一个正对角线矩阵(对角线元素大于0)$\boldsymbol{D}_0$,并且令
$$ \tilde{\boldsymbol{W}}_{kq}=\sqrt{d_k}\cdot \log\left(\boldsymbol{P}\cdot \boldsymbol{D}_0\right)\tag{7} $$
由于$\boldsymbol{P}$是一个正矩阵(矩阵内的元素都大于0),所以满足式(7)的$\tilde{\boldsymbol{W}}_{kq}$矩阵总是存在的,接下来我们证明$\boldsymbol{D}_{\tilde{\boldsymbol{W}}_{kq}}=\boldsymbol{D}_0$
$$ \boldsymbol{D}_{\tilde{\boldsymbol{W}}_{kq}}=\text{Diag}\left(\boldsymbol{1}^T\exp\left(\frac{\left(\tilde{\boldsymbol{W}}_{kq}\right)}{\sqrt{d_k}}\right)\right)=\text{Diag}\left(\boldsymbol{1}^T\boldsymbol{P}\cdot \boldsymbol{D}_0\right)=\boldsymbol{D}_0\tag{8} $$
最后一个等式成立,是因为$\boldsymbol{P}$的每一列和为1。最终,我们结合式(7)和式(8)
$$ \exp\left(\frac{\tilde{\boldsymbol{W}}_{kq}}{\sqrt{d_k}}\right)=\boldsymbol{P}\cdot \boldsymbol{D}_0=\boldsymbol{P}\cdot\boldsymbol{D}_{\tilde{\boldsymbol{W}}_{kq}}\tag{9} $$
接着我们证明$d<n$的情况。假设$d=1,n=2$,则$\boldsymbol{X}\in \mathbb{R}^{1\times 2},\boldsymbol{W}_q,\boldsymbol{W}_k,\boldsymbol{W}_v\in \mathbb{R}^{1\times 1}$,于是
$$ \text{Softmax}\left[\frac{\left(\boldsymbol{W}_{k} \boldsymbol{X}\right)^{T}\left(\boldsymbol{W}_{q} \boldsymbol{X}\right)}{\sqrt{d_{k}}}\right]=\text{Softmax}\left[\frac{[1,0]^{T} \boldsymbol{W}_{k}^{T} \boldsymbol{W}_{q}[1,0]}{\sqrt{d_{k}}}\right]=\operatorname{Softmax}\left[\left[\begin{array}{cc} \boldsymbol{W}_{k} \boldsymbol{W}_{q} & 0 \\ 0 & 0 \end{array}\right]\right]\tag{10} $$
这个矩阵很明显不符合我们对矩阵$\boldsymbol{P}$的要求,因为它的第二列元素无法做到不相等,或者说此时$\boldsymbol{P}$的秩很低
Multi-Head Attention
接着我们简单回顾一下Multi-Head Attenion,首先将Single-Head Attention中的一些变量重新进行定义
$$ \begin{aligned} \boldsymbol{W}_k\boldsymbol{X}\triangleq \boldsymbol{K}\\ \boldsymbol{W}_q\boldsymbol{X}\triangleq \boldsymbol{Q}\\ \boldsymbol{W}_v\boldsymbol{X}\triangleq \boldsymbol{V} \end{aligned} $$
于是则有
$$ \text{Attention}(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})=\text{Softmax}\left(\frac{\boldsymbol{Q}\boldsymbol{K}^T}{\sqrt{d_k}}\right)\boldsymbol{V}\tag{11} $$
其中$\boldsymbol{Q}\in \mathbb{R}^{n\times d_k},\boldsymbol{K}\in \mathbb{R}^{m\times d_k},\boldsymbol{V}\in \mathbb{R}^{m\times d_v}$。而Multi-Head Attention就是将$\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}$分别用$h$个不同的投影矩阵投影$h$次,然后分别做$h$次Single-Head Attention,最后把结果拼接起来,即
$$ \begin{equation}\begin{aligned}&\boldsymbol{Q}^{(1)}=\boldsymbol{Q}\boldsymbol{W}_Q^{(1)},\boldsymbol{K}^{(1)}=\boldsymbol{K}\boldsymbol{W}_K^{(1)},\boldsymbol{V}^{(1)}=\boldsymbol{V}\boldsymbol{W}_V^{(1)},\boldsymbol{O}^{(1)}=Attention\left(\boldsymbol{Q}^{(1)},\boldsymbol{K}^{(1)},\boldsymbol{V}^{(1)}\right)\\ &\boldsymbol{Q}^{(2)}=\boldsymbol{Q}\boldsymbol{W}_Q^{(2)},\boldsymbol{K}^{(2)}=\boldsymbol{K}\boldsymbol{W}_K^{(2)},\boldsymbol{V}^{(2)}=\boldsymbol{V}\boldsymbol{W}_V^{(2)},\boldsymbol{O}^{(2)}=Attention\left(\boldsymbol{Q}^{(2)},\boldsymbol{K}^{(2)},\boldsymbol{V}^{(2)}\right)\\ &\qquad\qquad\qquad\qquad\vdots\\ &\boldsymbol{Q}^{(h)}=\boldsymbol{Q}\boldsymbol{W}_Q^{(h)},\boldsymbol{K}^{(h)}=\boldsymbol{K}\boldsymbol{W}_K^{(h)},\boldsymbol{V}^{(h)}=\boldsymbol{V}\boldsymbol{W}_V^{(h)},\boldsymbol{O}^{(h)}=Attention\left(\boldsymbol{Q}^{(h)},\boldsymbol{K}^{(h)},\boldsymbol{V}^{(h)}\right)\\ &\boldsymbol{O}=\left[\boldsymbol{O}^{(1)},\boldsymbol{O}^{(2)},\dots,\boldsymbol{O}^{(h)}\right] \end{aligned}\tag{12}\end{equation} $$
Attention里有个瓶颈
在实际使用中,$\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}$一般具有相同的特征维度$d_k=d_v=d$(hidden_size),比如BERT-base里边是768;$h$一般选择12、16、24等,比如BERT-base里边是12;确定了$d,h$之后,通常的选择是让投影矩阵$\boldsymbol{W}\in \mathbb{R}^{d\times \frac{d}{h}}$,也就是说,每个Attention-Head里边,是将原始的$d$维投影到$\frac{d}{h}$维,然后再进行Attention运算,输出也是$\frac{d}{h}$维,最后把$h$个$\frac{d}{h}$维的结果拼接起来,得到一个$d$维的输出。这里的$\frac{d}{h}$我们通常称为head_size
在Attention中,关键的一步是
$$ \boldsymbol{P}=\text{Softmax}\left(\frac{\boldsymbol{Q}\boldsymbol{K}^T}{\sqrt{d_k}}\right)\tag{13} $$
在前面我们已经证明了,如果单个头的维度小于句子长度$n$,得到的$\boldsymbol{P}$并不好。那么这里单个头的维度是否小于$n$呢?很明显是的,就以BERT-base为例,$\frac{d}{h}=64\ll n$
不妨试试增大key_size?
那么,解决办法是什么呢?直接的想法是让$\frac{d}{h}$增大,所以要不就是减少head的数目$h$,要不就是增大hidden_size的大小$d$。但是更多的Attention Head本身也能增强模型的表达能力,所以为了缓解低秩瓶颈而减少$h$的做法可能得不偿失;如果增加$d$的话,那自然是能够增强模型整体表达能力的,但整个模型的规模与计算量也会剧增,似乎也不是一个好选择
难道没有其他办法了吗?有!当我们用投影矩阵将$\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}$都投影到低维时,前面都是将它们投影到$\frac{d}{h}$维,但其实它们的维度不一定要相等,而只需要保证$\boldsymbol{Q},\boldsymbol{K}$的维度相等就行了(因为要做内积),为了区别,我们通常称$\boldsymbol{Q},\boldsymbol{K}$的维度为key_size,$\boldsymbol{V}$的维度才叫head_size,改变key_size的大小而不改变head_size的话,也不影响模型的hidden_size
所以,这篇论文提出来的解决方法就是增大模型的key_size,它能增加Attention的表达能力,并且不改变模型整体的hidden_size,计算量上也只是稍微增加了一点
事实上原论文考虑的是同时增大key_size和head_size,Multi-Head Attention的输出拼接之后再用一个线性变换降维,但实际上只增大key_size也是有效果的
此外,如果同时增大key_size和head_size会导致计算量和显存明显增加,而只增大key_size的话,增加的资源消耗就小很多了
实验结果
增加key_size这个想法很简单,也很容易实现,但是否真的有效呢?我们来看看原论文的实验结果,其实验都是以BERT为baseline的,实验结果图表很多,推荐大家直接看原论文,这里只分享比较有代表性的一个
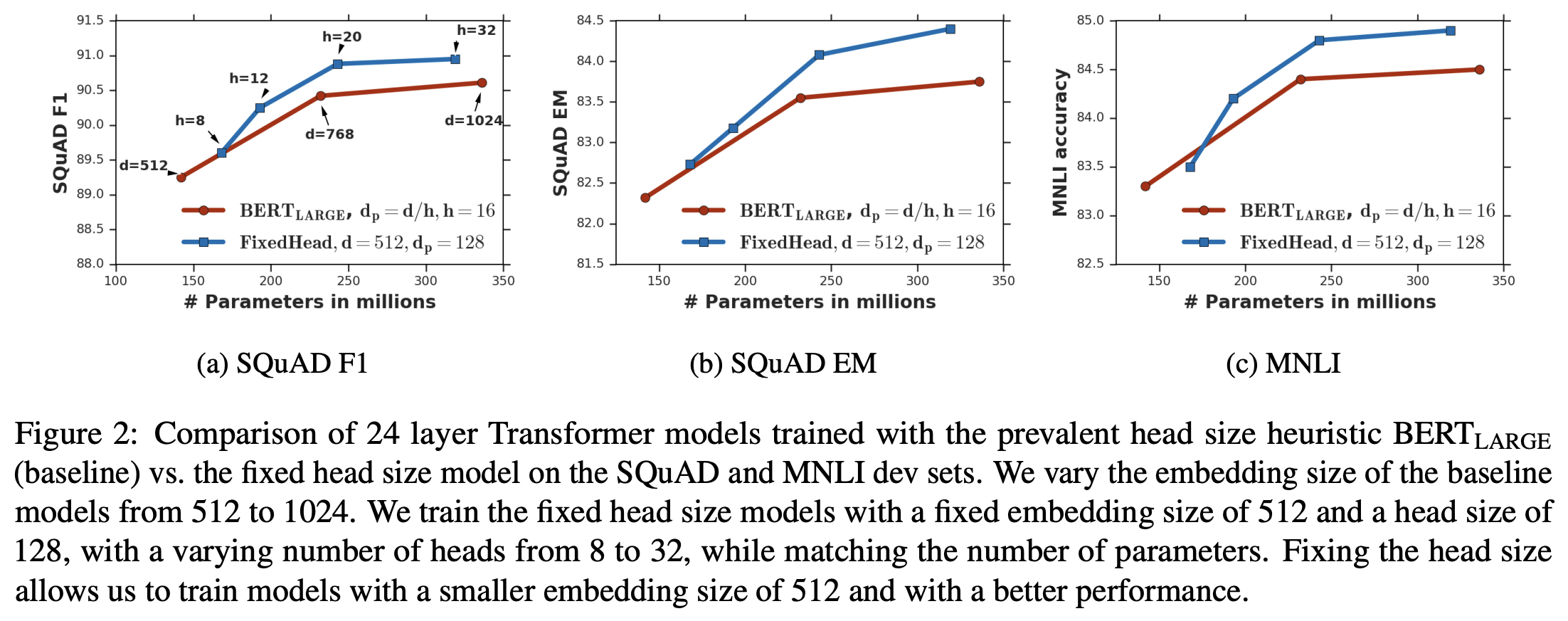
其中$d_p=\frac{d}{h}$。结果显示,如果固定一个比较大的key_size(比如128),那么我们可以调整模型的hidden_size和head数,使得参数量可以跟原始的BERT设计一致,但是效果更优!所以,增加key_size确实是有意义的,哪怕将总体参数量重新调整到原来的一样大,也能一定程度上提升模型的效果。这无疑对我们设计新的Transformer模型(尤其是小规模的模型)有重要的指导作用
再缺不能缺Talking
对Multi-Head Attention改进的第二个结果来自论文《Talking-Heads Attention》,这篇论文虽然没有显式地指出它跟前一篇论文的联系,但笔者认为它们事实上在解决同一个问题,只不过思路不一样:它指出当前的Multi-Head Attention每个head的运算是相互孤立的,而通过将它们联系(Talking)起来,则可以得到更强的Attention设计,即标题的"Talking-Heads Attention"
从单一分布到混合分布
在前一篇论文里边,我们提到了低秩瓶颈,也就是由于key_size太小,所以$(\boldsymbol{Q}^{(i)}\boldsymbol{K}^{(i)})^T$表达能力不足。为了缓解这个问题,除了增大key_size之外,还有没有其他方法呢?有,比如这篇文论使用的混合分布思路
所谓混合分布,就是多个简单分布的叠加(比如加权平均),它能极大的增强原分布的表达能力。典型的例子是高斯混合模型:我们知道高斯分布只是一个常见的简单分布,但多个高斯分布叠加而成的高斯混合分布(也叫高斯混合模型,GMM)就是一个更强的分布,理论上来说,只要叠加的高斯分布足够多,高斯混合分布能逼近任意概率分布。这个例子告诉我们,想要增加Attention中分布的表达能力,又不想增加key_size,那么可以考虑叠加多个低秩分布
那么"多个"低秩分布哪里来呢?不是有Multi-Head嘛,每个head都带有一个低秩分布,就直接用它们叠加就行了,这就是Talking-Heads Attention。具体来说,它的形式是:
$$ \begin{equation}\begin{aligned}&\hat{\boldsymbol{J}}^{(1)}=\boldsymbol{Q}^{(1)}{\boldsymbol{K}^{(1)}}^{T},\quad\hat{\boldsymbol{J}}^{(2)}=\boldsymbol{Q}^{(2)}{\boldsymbol{K}^{(2)}}^{T},\quad\cdots,\quad\hat{\boldsymbol{J}}^{(h)}=\boldsymbol{Q}^{(h)}{\boldsymbol{K}^{(h)}}^{T}\\ &\begin{pmatrix}\boldsymbol{J}^{(1)} \\ \boldsymbol{J}^{(2)} \\ \vdots \\ \boldsymbol{J}^{(h)}\end{pmatrix}=\begin{pmatrix}\lambda_{11} & \lambda_{12}& \cdots & \lambda_{1h}\\ \lambda_{21} & \lambda_{22} & \cdots & \lambda_{2h}\\ \vdots & \vdots & \ddots & \vdots\\ \lambda_{h1} & \lambda_{h2} & \cdots & \lambda_{hh} \end{pmatrix}\begin{pmatrix}\hat{\boldsymbol{J}}^{(1)} \\ \hat{\boldsymbol{J}}^{(2)} \\ \vdots \\ \hat{\boldsymbol{J}}^{(h)}\end{pmatrix}\\ &\boldsymbol{P}^{(1)}=softmax\left(\boldsymbol{J}^{(1)}\right),\boldsymbol{P}^{(2)}=softmax\left(\boldsymbol{J}^{(2)}\right),\dots,\boldsymbol{P}^{(h)}=softmax\left(\boldsymbol{J}^{(h)}\right)\\ &\boldsymbol{O}^{(1)}=\boldsymbol{P}^{(1)} \boldsymbol{V}^{(1)},\quad \boldsymbol{O}^{(2)}=\boldsymbol{P}^{(2)} \boldsymbol{V}^{(2)},\quad ,\cdots,\quad\boldsymbol{O}^{(h)}=\boldsymbol{P}^{(h)} \boldsymbol{V}^{(h)}\\ &\boldsymbol{O}=\left[\boldsymbol{O}^{(1)},\boldsymbol{O}^{(2)},\dots,\boldsymbol{O}^{(h)}\right] \end{aligned}\tag{14}\end{equation} $$
写起来很复杂,事实上很简单,就是在$\boldsymbol{Q}\boldsymbol{K}^T$之后、Softmax之前,用一个参数矩阵$\lambda$将各个$\boldsymbol{Q}\boldsymbol{K}^T$的结果叠加一下而已。这样就把原本是孤立的各个Attention Head联系了起来,即做了一个简单的Talking
对上述公式做两点补充说明:
- 简单起见,上述公式中笔者省去了缩放因子$\sqrt{d_k}$,如有需要,读者自行补充上去即可
- 更一般的Talking-Heads Attention允许在$\boldsymbol{J}=\lambda\hat{J}$这一步进行升维,即叠加出多于$h$个混合分布,然后再用另一个参数矩阵降维,但这并不是特别重要的改进,所以不做主要介绍
实验结果
是不是真的有效,当然还是得靠实验结果来说话。这篇论文的实验阵容可谓空前强大,它同时包含了BERT、ALBERT、T5为baseline的实验结果!众所周知,BERT、ALBERT、T5均是某个时间段的NLP最优模型,尤其是T5还是处在superglue的榜首,并且远超出第二名很多,而这个Talking-Heads Attention则几乎是把它们的辉煌战绩又刷到了一个新高度!
还是那句话,具体的实验结果大家自己看论文,这里展示一个比较经典的结果:

结果显示,使用Talking-Head Attention情况下,保持hidden_size不变,head数目越大(相应地key_size和head_size都越小),效果越好。这看起来跟前一篇增大key_size的结论矛盾,但是事实上这正说明了混合分布对分布拟合能力具有明显的提升作用,能将key_size缩小时本身变弱的单一分布,叠加成拟合能力更强大的分布。当然,这不能说明直接设key_size=1就好了,因为key_size=1时计算量会远远大于原始的BERT-base,应用时需要根据实际情况平衡效果和计算量
上述表格只是原论文实验的冰山一角,这里再放出一个实验表格,让大家感受感受它的实验阵容:

几乎每个任务、每个超参数组合都做了实验,并给出实验结果。如此强大的实验阵容,基本上也就只有Google能搞出来了

请问一下博主有用Talking-Head Attention做过实验吗?为什么感觉我用多头注意力机制做文本分类实验的效果要比Talking-Head Attention效果还要好,在两个的数据集下我试过48,64,100头的准确率提示的都没多头注意力好@(泪)@(泪)