概述展开目录
Cache 即高速缓存，是用来解决主存与 CPU 速度不匹配的问题，Cache 的出现使得 CPU 可以不直接访问主存而直接与 Cache 交换信息。由于程序访问的局部性原理可以很容易设想只要将 CPU 近期要用到的程序和数据提前从主存送到 Cache, 那么就可以做到 CPU 在一定时间内只访问 Cache，这样 CPU 与高速 Cache 进行通信，就大大提高了计算机的运行速度
程序的局部性原理： 局部性原理又表现为：时间局部性和空间局部性。时间局部性是指如果程序中的某条指令一旦执行，则不久之后该指令可能再次被执行；如果某数据被访问，则不久之后该数据可能再次被访问。空间局部性是指一旦程序访问了某个存储单元，则不久之后。其附近的存储单元也将被访问。
Cache 的工作原理展开目录
在 Cache 与主存的地址映射之前，首先要将主存与 Cache 都分成若干块，每块又包括若干个字，并使得它们的大小相同（即块内的字数相同，因为 Cache 与主存之间的数据交互是以行为单位，所以他俩每行存储的字大小必须相同）。
在划分好块后，下面要做的就是将主存块与 Cache 块形成映射就行了。而这里的映射则是通过块的地址形成映射关系。对于地址映射，首先将主存地址分成两块，高 $m$ 位为主存的快地址，低 $b$ 位为块内地址。（字块中存放的就是真正使用的数据，只是映射时使用地址来映射）
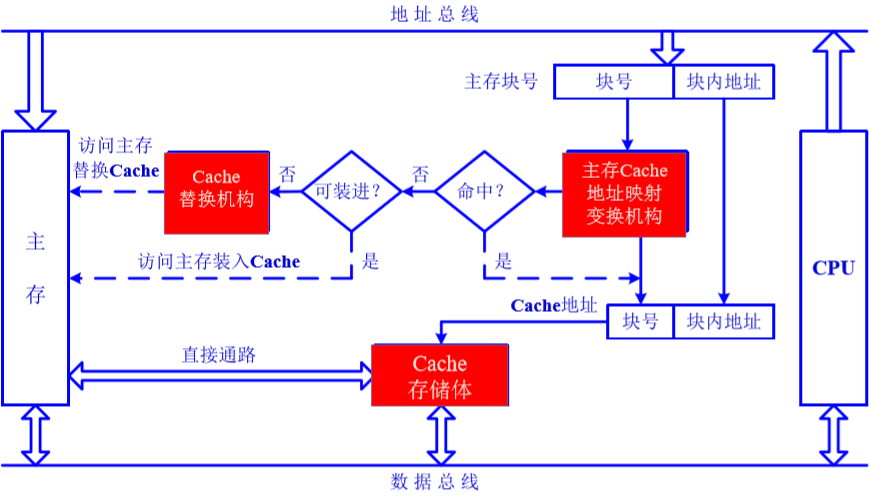
Cache 的读写操作展开目录
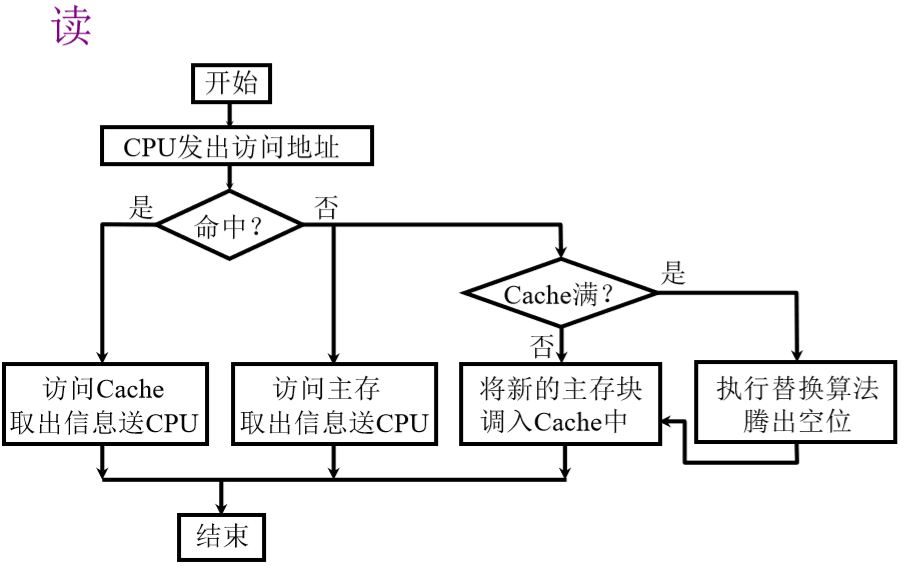
Cache 命中率展开目录
在一个程序执行期间，设 Nc 表示 cache 完成存取的次数，Nm 表示主存完成存取的次数，h 表示 cache 的命中率，则：
$$ h = \frac{Nc}{Nc+Nm} $$
cache / 主存系统的平均访问时间展开目录
若 $t_c$ 表示命中时 cache 的访问时间，$t_m$ 表示未命中时主存的访问时间，h 表示 cache 的命中率，$t_a$ 表示平均访问时间，则：
$$ t_a = ht_c+(1-h)t_m $$
访问效率展开目录
$$ e = \frac{t_c}{t_a} = \frac{t_c}{ht_c+(1-h)t_m}=\frac{1}{h+(1-h)r} = \frac{1}{r+(1-r)h} $$
其中，$r=\frac {t_m}{t_c}$
关于 Cache 命中率有一个坑，提前给出来，免得以后犯错。$t_m$ 的定义是 “未命中时主存访问的时间”，所以不能单纯的理解为 “主存的存储周期”，比如下面一道题
某计算机的存储系统采用由 cache - 主存系统构成，cache 的存储周期为 10ns，主存的存储周期为 50ns。若 CPU 执行一段程序时，cache 完成存取的次数为 4800 次，主存完成存取的次数为 200 次，cache 与主存不能同时访问，求该 cache - 主存系统的访问效率。
习惯地认为这里 “$t_m=50ns$”，但是请注意一句话 “cache 与主存不能同时访问”，$t_m$ 的定义是 “未命中时主存的访问时间”，既然 “未命中”，说明在该题的情景下，先访问了 cache，用了 10ns，再去访问主存。所以：$t_m=10+50=60ns$
Cache 与主存的映射方式展开目录
Cache 与主存的地址映射方式有很多，有直接映射，全相联映射，组相联映射。
1. 直接映射展开目录
在这种映射方式下，主存中的任一块只与一个缓存块相对应，映射关系为：$i = j mod C$，其中，$i$ 为缓存块号，$j$ 为主存块号，$C$ 为缓存块数。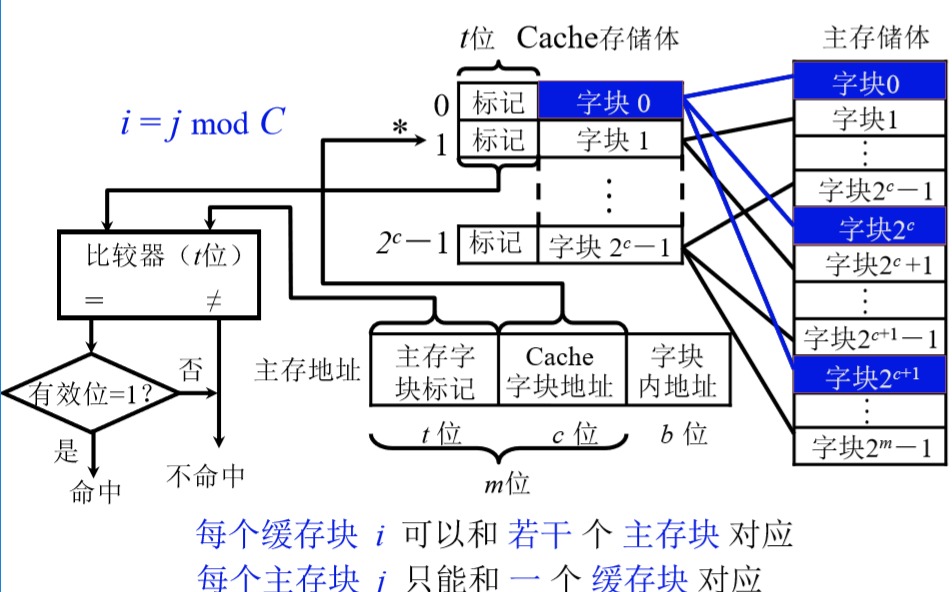
当缓存接收到 CPU 发送来的主存地址后，只需根据中间 c 位字段 (假设为 00…01) 找到缓存块 1, 然后根据字块 1 的 “标记” 是否与主存地址的高 t 位相符合，若符合且有效位为 1 (这里的有效位用来识别 Cache 存储块中的额数据是否有效，因为有时 Cache 中的数据是无效的，例如，在初始时刻 Cache 中的额内容为空，是无意义的)，则表示该 Cache 块已和主存中的某块建立了对应关系，则可根据 b 位块内地址从 Cache 块中取得对应的字，即找到 CPU 发来的主存地址在缓存中所对应的信息；若不符合，或者有效位为”0”，则主存读入新的字块来代替旧的字块，同时将信息送往 CPU，并修改 Cache “标记”。
特点： 不灵活，每个主存块只能按照取模固定地映射到某个缓存块，即使缓存内其他块空着，也不能用来映射。因而如果程序恰好要重复地使用对应同一缓存块的不同主存块，那么久需要不同的替换，这样会降低命中率。
2. 全相联映射展开目录
全相联映射中，主存的任一块可以放到任一缓存块中。这样 CPU 如果获取主存的内的数据，就需要扫描整个缓存，看当前缓存中是否包含有所需的主存的数据
特点： 全相联映射允许将主存中的每一字块映射到 Cache 中的任意一块位置上。显然这种映射方式相对于直接映射，更加灵活，命中率也更高，缩小了块冲突。同时也因为这个特点，所需的逻辑电路较多，成本也比较高。
3. 组相连映射展开目录
针对上述直接映射和全相联映射出现的问题，现在出现一种折中的映射方式，即下面介绍的组相联映射。该映射方式将所有 Cache 分为 Q 组，每组有 R 块，则有关系：$i = j mod Q$，其中 $i,j$ 的含义与直接映射中的含义一致
之所以说是折中，是因为按照直接映射中取模的方式，某个主存块映射到 Cache 中的组是固定的，但是在组内，又按照全相联映射原则，“随意存放”，即通过主存字块标记可以映射到该组中任意一块 Cache 块。
这里看似主存地址很复杂，其实只要知道 Cache 一共有多少组即可确定组地址的位数，字块内地址与前面两种映射方式所说的一致，最后通过总位数减去组地址位数和字块内地址位数即得主存字块标记位数。
常用替换算法展开目录
Cache miss 不仅意味着需要从主存获取数据，而且还需要将 cache 的某一块替换出去。常用的算法包括 FIFO、LRU、LFU、Random 等
FIFO: First in First out展开目录
假如依次进入 Cache 的数据为：1、5、4、3、2，如果此时 Cache 满了，又有一个新的数据 6 要进入，此时就会将数据 1 所在的块清空，把 6 放进来；如果 1 这个数据又来了，那么就会将 5 所在的数据块清空，把 1 放进来
Radom展开目录
这个就是纯粹的玄学随机移除，如果 Cache 满了，随机移除某一块
LFU展开目录
LFU（Least Frequently Used）最近最不常用算法。它是基于如果一个数据在最近一段时间内使用次数很少，那么在将来一段时间内被使用的可能性也很小的思路
假设缓存大小为 3，数据访问序列为 set (2,2),set (1,1),get (2),get (1),get (2),set (3,3),set (4,4)
则在 set (4,4) 时对于 LFU 算法应该淘汰 (3,3)
实现思路：每行设置一个计数器，计数器最小的行将被替换
LRU展开目录
LRU（Least Recently Used）最近最少使用。它是基于：如果一个数据在最近一段时间没有被访问到，那么在将来它被访问的可能性也很小。也就是说，当限定的空间已存满数据时，应当把最久没有被访问到的数据淘汰。
注意 LFU 和 LRU 算法的不同之处，LRU 的淘汰规则是基于访问时间，而 LFU 是基于访问次数的。
假设缓存大小为 3，数据访问序列为 set (2,2),set (1,1),get (2),get (1),get (2),set (3,3),set (4,4)
LRU 应该淘汰 (1,1)
实现思路：每行设置一个计数器，Cache 命中相应的计数器清零，其他计数值加 1，计数值最大的行将被替换
小结展开目录
直接映射：某一主存块只能固定映射到某一缓存块
全相联：某一主存块能映射到任一缓存块
组相联：某一主存块只能映射到某一缓存组中的任一块
