神经网络算法

人工神经网络概述

生物神经元

人工神经元

人工神经元用于模拟生物神经元，人工神经元可以看做是一个多输入、单输出的信息处理单元，它先对输入变量进行线性组合，然后对组合的结果做非线性变换。因此可以将神经元抽象为一个简单的数学模型，也称为感知器。

最简单的人工神经元模型:

神经元的工作过程一般是：

• 从各输入端接收输入信号xi
• 根据连接权值wi，求出所有输入的加权和，即$net=\sum_{i=1}^nw_ix_i$
• 对$net$做非线性变换，得到神经元的输出，即$y=f(net)$

$f$称为激活函数或激励函数，它对该神经元所获得输入进行变换，反映神经元的特性。常用的激活函数类型如下：

• 线性函数 $f(x)=kx+c$
• 符号函数
• 对数函数 $f(x)=\frac{1}{1+e^{-x}}$

对数函数又称S形函数，其图形如下图所示，是最为常用的激活函数，它将$(-∞，+∞)$区间映射到（0，1）的连续区间。特别地，$f(x)$是关于$x$处处可导的，并有$f(x)$的导数$f'(x)=f(x)(1-f(x))$

人工神经网络

神经网络由3个要素组成：拓扑结构、连接方式和学习规则

1.拓扑结构

拓扑结构是一个神经网络的基础。拓扑结构可以是两层或者两层以上的。如下图是一个两层神经网络，它只有一组输入单元和一个输出单元，是最简单的神经网络结构

2.连接方式

神经网络的连接包括层之间的连接和每一层内部的连接，连接的强度用权表示。不同的连接方式构成了网络的不同连接模型。常见的有以下几种：

• 前馈神经网络
• 反馈神经网络
• 层内有互连的神经网络

前馈神经网络

前馈神经网络也称前向神经网络，其中单元分层排列，分别组成输入层、隐藏层和输出层，每一层只接受来自前一层单元的输入，无反馈。如下图所示的是一个两层前馈神经网络，图中箭头表示连接方向。

反馈神经网络

在反馈神经网络中，除了单向连接外，最后一层单元的输出返回去作为第一层单元的输入。如下图所示的是一个两层反馈神经网络。

层内有互连的神经网络

在前面两种神经网络中，同一层的单元都是相互独立的，不发生横向联系。有些神经网络中同一层的单元之间存在连接

3.学习规则

神经网络的学习分为离线学习和在线学习两类

• 离线学习指神经网络的学习过程和应用过程是独立的
• 在线学习指学习过程和应用过程是同时进行的

神经网络应用

神经网络方法应用于实际问题的一般过程如下：

1. 神经网络在开始训练之前，必须设计好神经网络的拓扑结构，包括输入层的单元数、隐藏层数（如果多于一层）、每一隐藏层的单元数和输出层的单元数，单元之间的连接方式，以及每个单元激活函数的选取。同时需要对网络连接的权值和每个单元的偏置进行初始化。
2. 然后进行训练样本学习，计算各层连接权值和偏置值。
3. 最后是工作阶段，用确定好的神经网络解决实际分类问题。

用于分类的前馈神经网络

前馈神经网络的学习过程

前馈神经网络广泛使用的学习算法是由Rumelhart等人提出的误差后向传播（Back Propagation，BP）算法。

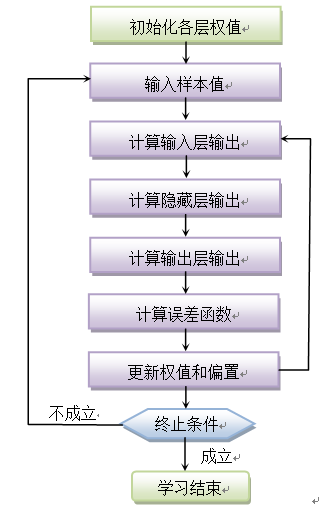
BP算法的学习过程分为两个基本子过程，即工作信号正向传递子过程和误差信号反向传递子过程，如下图所示：

计算过程

BP神经网络的计算过程由正向计算过程和反向计算过程组成。

正向传播过程，输入模式从输入层经隐单元层逐层处理，并转向输出层，每一层神经元的状态只影响下一层神经元的状态。

如果在输出层不能得到期望的输出，则转入反向传播，将误差信号沿原来的连接通路返回，通过s修改各神经元的权值，使得误差信号最小。

1.工作信号正向传递子过程

输入层的输入向量为$X=(x_1,x_2,…,x_n)$，隐藏层输出向量$Y=(y_1,y_2,…,y_m)$，并有：

$$ \begin{align} net_j = \sum_{i = 1}^{n}v_{ij}x_i+\theta_j \\ y_j = f(net_j) = \frac{1}{1+e^{-net_j}} \end{align} $$

其中，偏置$\theta_j$是隐藏层中节点$j$用来改变单元的活性的阈值。同样地，输出层输出向量$O=(o_1,o_2,…,o_l)$，并有：

$$ \begin{align} net_k = \sum_{j = 1}^{m}w_{jk}y_j+\theta_k \\ o_k = f(net_k) = \frac{1}{1+e^{-net_k}} \end{align} $$

这样，$O$向量就是输入向量$X$对应的实际输出，$o_k$是输入向量$X$对应的第$k$个输出单元的输出。

2. 误差信号反向传递子过程

为了降低推导过程的复杂性，在下面讨论一次误差信号反向传递，计算权修改量$\triangle w_{jk}$、$\triangle v_{ij}$时不考虑偏置$\theta_k$和$\theta_j$，这不影响权修改量的计算结果。

对于某个训练样本，实际输出与期望输出存在着误差，用误差平方和来表示误差信号即$E$定义为：

$$ E=\frac{1}{2}(d-o)^2=\frac{1}{2}\sum_{k=1}^{l}(d_k-o_k)^2 $$

其中$d_k$是输出层第$k$个单元基于训练样本的期望输出（也就是该训练样本真实类别对应的输出），$o_k$是该样本在训练时第$k$个单元的实际输出。

将以上误差信号向后传递回隐藏层，即将以上定义式$E$展开到隐藏层：

$$ E=\frac{1}{2}\sum_{k=1}^{l}(d_k-o_k)^2=\frac{1}{2}\sum_{k=1}^{l}[d_k-f(net_j)]^2=\frac{1}{2}\sum_{k=1}^{l}[d_k-f(\sum_{j=1}^{m}w_{jk}y_j)]^2 $$

再将误差信号向后传递回输入层，即将以上定义式$E$进一步展开至输入层：

$$ E=...=\frac{1}{2}\sum_{k=1}^{l}\{d_k-f[\sum_{j=1}^mw_{jk}f(\sum_{i=1}^{n}v_{ij}x_i)]\}^2 $$

从中看到，误差平方和$E$取决于权值$v_{ij}$和$w_{jk}$，它是权值的二次函数。

为了使误差信号$E$最快的减少，采用梯度下降法，$E$是一个关于权值的函数，$E(w_{jk})$在某点$w_{jk}$的梯度$\triangle E(w_{jk})$是一个向量，其方向是$E(w_{jk})$增长最快的方向。显然，负梯度方向是$E(w_{jk})$减少最快的方向。在梯度下降法中，求某函数极大值时，沿着梯度方向走，可以最快达到极大点；反之，沿着负梯度方向走，则最快地达到极小点。

为使函数$E(w_{jk})$最小化，可以选择任意初始点$w_{jk}$，从$w_{jk}$出发沿着负梯度方向走，可使得$E(w_{jk})$下降最快，所以取：

$$ \triangle w_{jk}=-\eta \frac{\partial E}{\partial w_{jk}},j=1...m,k=1...l $$

其中$\eta$是一个学习率，取值为0～1。

同样的

$$ \triangle v_{ij}=-\eta \frac{\partial E}{\partial v_{ij}},j=1...m,k=1...l $$

对于输出层的$\triangle w_{jk}$：

$$ \triangle w_{jk}=-\eta \frac{\partial E}{\partial w_{jk}}=-\eta \frac{\partial E}{\partial net_k} \times \frac{\partial net_k}{\partial w_{jk}}=-\eta \frac{\partial E}{\partial net_k} \times y_j $$

对于隐藏层的$\triangle v_{ij}$：

$$ \triangle v_{ij}=-\eta \frac{\partial E}{\partial v_{ij}}=-\eta \frac{\partial E}{\partial net_{jk}} \times \frac{\partial net_j}{\partial v_{ij}}=-\eta \frac{\partial E}{\partial net_{jk}} \times x_i $$

对输出层和隐藏层各定义一个权值误差信号，令：

$$ \delta^o_k=-\frac{\partial E}{\partial net_k},\delta^y_j=-\frac{\partial E}{\partial net_j} $$

则$\delta w_{jk}=\eta \delta^o_k y_j,\delta v_{ij}=\eta \delta^y_j x_i$

只要计算出$\delta^o_k,\delta^y_j$，则可计算出权值调整则$\delta w_{jk}$和$\delta v_{ij}$

对于输出层$\delta^o_k$可展开为：

$$ \delta^o_k=-\frac{\partial E}{\partial net_k}=-\frac{\partial E}{\partial o_k} \times \frac{\partial o_k}{\partial net_k} = -\frac{\partial E}{\partial o_k} \times f'(net_k) $$

对于隐藏层$\delta^y_j$可展开为：

$$ \delta^y_j=-\frac{\partial E}{\partial net_j}=-\frac{\partial E}{\partial y_j} \times \frac{\partial y_j}{\partial net_j} = -\frac{\partial E}{\partial y_j} \times f'(net_j) $$

由于$E=\frac{1}{2}\sum_{k=1}^{l}[d_k-f(\sum_{j=1}^{m}w_{jk}y_j)]^2$可得：

$$ \begin{align} \frac{\partial E}{\partial o_k}=-(d_k-o_k),\frac{\partial E}{\partial y_j}=-\sum_{k=1}^{l}(d_k-o_k)f'(net_k)w_{jk} \end{align} $$

由$o_k=f(net_k)=\frac{1}{1+e^{-net_k}},f(x)$的导数$f'(x)=f(x)(1-f(x))$，可求出$f'(net_k)=o_k(1-o_k)$，代入可得：

$$ \delta^o_k=-\frac{\partial E}{\partial o_k} \times f'(net_k)=(d_k-o_k)o_k(1-o_k) $$

同样推出

$$ \delta^y_j=-\frac{\partial E}{\partial y_j} \times f'(net_j)=(\sum_{k=1}^{l}\delta^o_kw_{jk})y_j(1-y_j) $$

所以前馈神经网络BP学习算法权值调整计算公式如下：

$$ \begin{align} & \delta^o_k=(d_k-o_k)o_k(1-o_k)\\ & \triangle w_{jk}=\eta \delta^o_k y_j \\ & \delta^y_j =(\sum_{k=1}^{l}\delta^o_kw_{jk})y_j(1-y_j) \\ &\triangle v_{ij} = \eta \delta^y_j x_i \end{align} $$

再考虑各层的偏置设置，隐藏层的净输出为：

$$ net_j = \sum_{i=1}^{n}v_{ij}x_i+\theta_j $$

隐藏层偏置的更新为（$\triangle \theta_j$是偏置$\theta_j$的改变）：

$$ \triangle \theta_j=\eta \delta^o_k,\theta_j=\theta_j+\triangle \theta_j $$

相应地，输出层地净输出为：

$$ net_j=\sum_{i=1}^{m}w_{ij}y_i+\theta_j $$

输出层偏置的更新为（$\triangle \theta_j$是偏置$\theta_j$的改变）：

$$ \triangle \theta_j = \eta \delta^y_j,\theta_j = \theta_j+\triangle \theta_j $$

上述过程是一个样本训练的一次迭代，通过多个样本的多次迭代，直到找到合适的权值和偏置为止。

BP神经网络的优劣势

BP神经网络无论在网络理论还是在性能方面已比较成熟。其突出优点就是具有很强的非线性映射能力和柔性的网络结构。网络的中间层数、各层的神经元个数可根据具体情况任意设定，并且随着结构的差异其性能也有所不同。但是BP神经网络也存在以下的一些主要缺陷：

• 学习速度慢，即使是一个简单的问题，一般也需要几百次甚至上千次的学习才能收敛。
• 容易陷入局部极小值。
• 网络层数、神经元个数的选择没有相应的理论指导。
• 网络推广能力有限。

应用

目前，在人工神经网络的实际应用中，绝大部分的神经网络模型都采用BP网络及其变化形式。它也是前向网络的核心部分，体现了人工神经网络的精华。

BP网络主要用于以下四个方面：

1. 函数逼近：用输入向量和相应的输出向量训练一个网络逼近一个函数。
2. 模式识别：用一个待定的输出向量将它与输入向量联系起来。
3. 分类：把输入向量所定义的合适方式进行分类。
4. 数据压缩：减少输出向量维数以便于传输或存储

例题

有如下图所示的一个简单的前馈神经网络，输入层有3个单元，编号为0～2，隐藏层只有一层，共2个单元，编号为0、1，输出层仅有一个单元，编号为0。其中$ee_j$表示隐藏层的误差信号，$eo_k$表示输出层的误差信号 ，$θ_e$表示隐藏层的偏置，$θ_o$表示输出层的偏置。假设学习率$\eta=0.9$。并规定迭代结束条件是：当某次迭代结束时，所有权改变量都小于某个指定阈值0.01，则训练终止。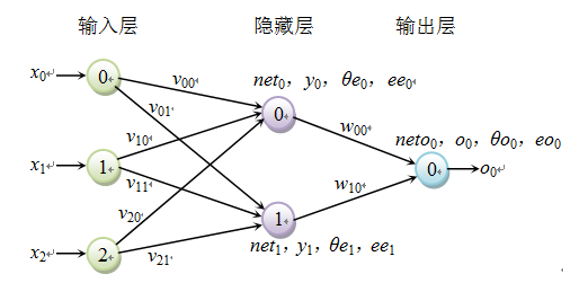

现有一个训练样本$s$，它的输入向量为（1,0,1），类别为1。采用上述算法的学习过程如下：

（1）随机产生权值和偏置值，假设结果如下表所示

（2）第一次迭代
①求隐藏层输出

$$ \begin{align} & net_0=\sum v_{i0}\times x_i=(0.2\times 1)+(0.4\times 0)+(-0.5 \times 1)+(-0.4)=0.7 \\ & y_0=\frac{1}{1+e^{-net_0}}=0.331812 \\ & net_1=\sum v_{i1}\times x_i=(-0.3\times 1)+(0.1\times 0)+(0.2 \times 1)+0.2=0.1 \\ & y_1=0.524979 \end{align} $$

②求输出层输出

$$ neto_0=\sum w_{i0}\times y_i = (-0.3 \times 0.331812)+(-0.2 \times 0.524979) + 0.1 = -0.10454 \\ o_0 = 0.47889 $$

③求输出层误差信号

$$ eo_0=(1-0.473889)\times 0.473889\times (1-0.473889)=0.131169 $$

④求隐藏层误差信号

$$ \begin{align} & ee_0=0.131169\times (-0.3) \times 0.331812 \times (1-0.331812) = -0.00872456 \\ & ee_1=(0.131169 \times (-0.2) \times 0.524979)\times (1-0.524979)=-0.00654209 \end{align} $$

⑥求输入层权该变量和新权

$$ \begin{align} & \triangle v_{00}=0.9\times(-0.00872456)\times 1=-0.00785211 \\ & v_{00}=0.2+(-0.00785211)=0.192148 \\ & \triangle v_{01}=0.9\times(-0.00654209)\times 1=-0.00588788 \\ & v_{01}=-0.3+(-0.00588788)=-0.305888 \\ & \triangle v_{10}=0.9\times(-0.00872456)\times 0=0 \\ & v_{10}=0.4+0=0.4 \\ & \triangle v_{11}=0.9\times(-0.00654209)\times 0=0 \\ & v_{11}=0.1+0=0.1 \\ & \triangle v_{20}=0.9\times(-0.00872456)\times 1=0.00785211 \\ & v_{20}=-0.5+(-0.00785211)=-0.507852 \\ & \triangle v_{21}=0.9\times(-0.00654209)\times 1=-0.00588788 \\ & v_{21}=0.2+(-0.00588788)=0.194112 \\ \end{align} $$

⑦求隐藏层每个单元的偏置该变量和新偏置

$$ \begin{align} & \triangle \theta e_0=0.9\times (-0.00872456)=-0.00785211 \\ & \theta e_0=-0.4+(0.00785211)=-0.407852 \\ & \triangle \theta e_1=0.9\times (-0.00654209)=-0.00588788 \\ & \theta e_1=0.2+(-0.0058788)=0.194112 \\ & \triangle \theta o_0=0.9\times 0.131169=0.118052 \\ & \theta o_0=0.1+0.118052=0.218052 \end{align} $$

后面多次迭代的过程就不写了

前馈神经网络、BP神经网络、卷积神经网络的区别与联系

前馈神经网络

前馈神经网络就是一层的节点只有前面一层作为输入，并输出到后面一层，自身之间、与其它层之间都没有联系，由于数据是一层层向前传播的，因此称为前馈网络。

BP神经网络

BP网络是最常见的一种前馈网络，BP体现在运作机制上，数据输入后，一层层向前传播，然后计算损失函数，得到损失函数的残差，然后把残差向后一层层传播。

卷积神经网络

卷积神经网络是根据人的视觉特性，认为视觉都是从局部到全局认知的，因此不全部采用全连接（一般只有1-2个全连接层，甚至最近的研究建议取消CNN的全连接层），而是采用一个滑动窗口只处理一个局部，这种操作像一个滤波器，这个操作称为卷积操作（不是信号处理那个卷积操作，当然卷积也可以），这种网络就称为卷积神经网络。

三者之间的关系

目前流行的大部分网络就是前馈网络和递归网络，这两种网络一般都是BP网络；深度网络一般采用卷积操作，因此也属于卷积神经网络。在出现深度学习之前的那些网络，基本都是全连接的，则不属于卷积网络的范围，但大部分是前馈网络和BP网络。