时间序列
时间序列（简称为时序）是指同一现象在不同时间上的相继观测值排列而成的数列，一个按时间顺序排列的数列，形式上由现象所属的时间和现象在不同时间上的观测值两部分组成，排列的时间可以是年份、季度、月份或其他任何时间形式。
时间序列分析
时间序列分析是一种动态数据处理的统计方法。该方法基于随机过程理论和数理统计学方法，研究随机数据序列所遵从的统计变化规律，以用于解决实际问题。通常影响时间序列变化的4个要素如下：
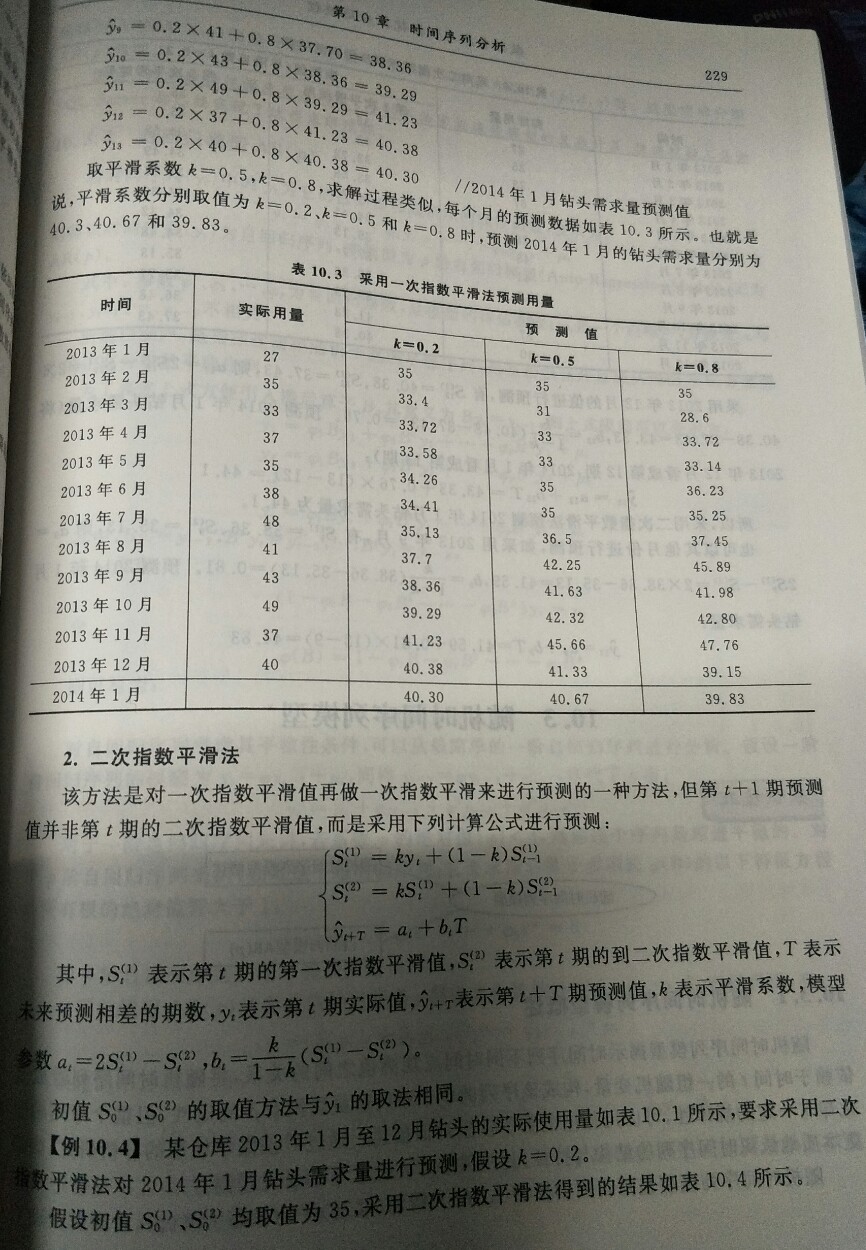
- 长期趋势：是时间序列在长时期内呈现出来的持续向上或持续向下的变动。
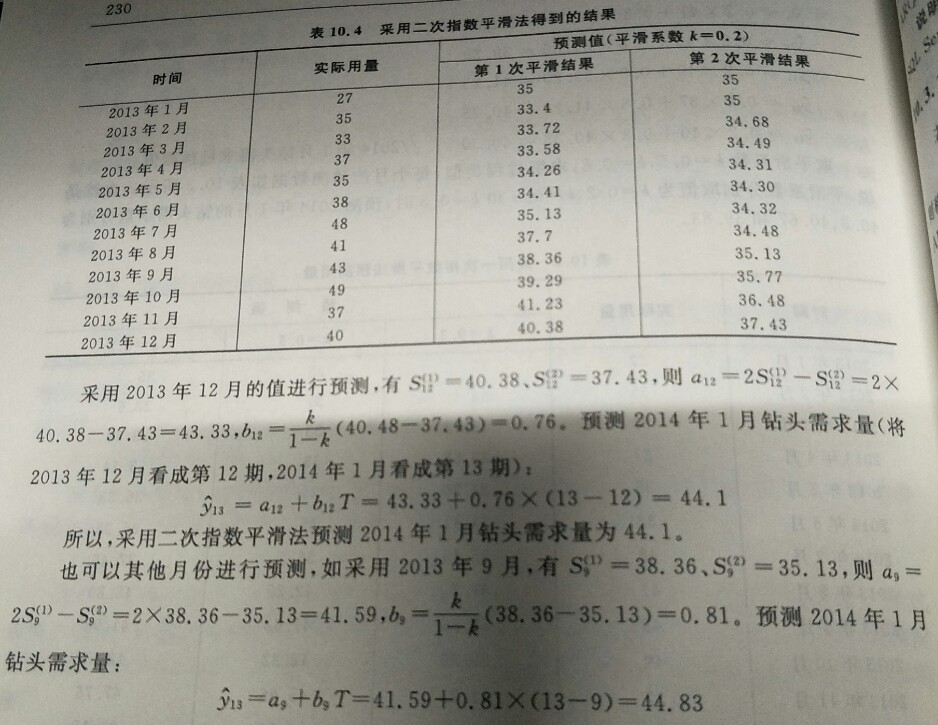
- 季节变动：是时间序列在一年内重复出现的周期性波动。
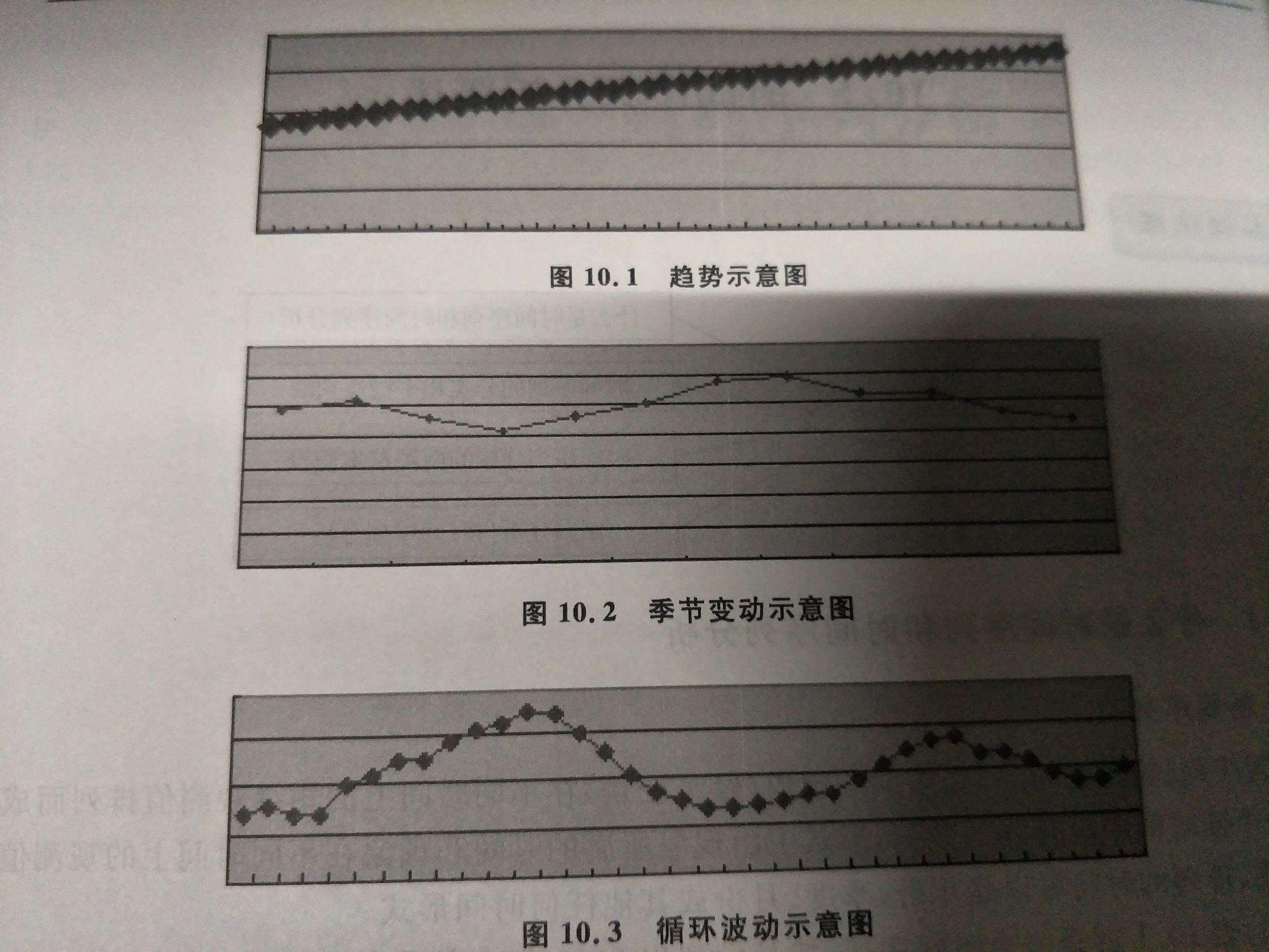
- 循环波动：是时间序列呈现出得非固定长度的周期性变动。
- 不规则变化。是时间序列中除去长期趋势、季节变动和循环波动之后的随机波动。不规则波动通常总是夹杂在时间序列中，致使时间序列产生一种波浪形或震荡式的变动。
时间序列的分类和平稳性判断方法
时间序列的分类
时间序列可以分为平稳序列和非平稳序列。
平稳序列是指基本上不存在长期趋势的序列，各观测值基本上在某个固定的水平上波动，或虽有波动，但并不存在某种规律，而其波动可以看成是随机的。或者说只含有随机波动的序列称为平稳序列。
非平稳序列是指有长期趋势、季节性和循环波动的复合型序列，其趋势可以是线性的，也可以是非线性的。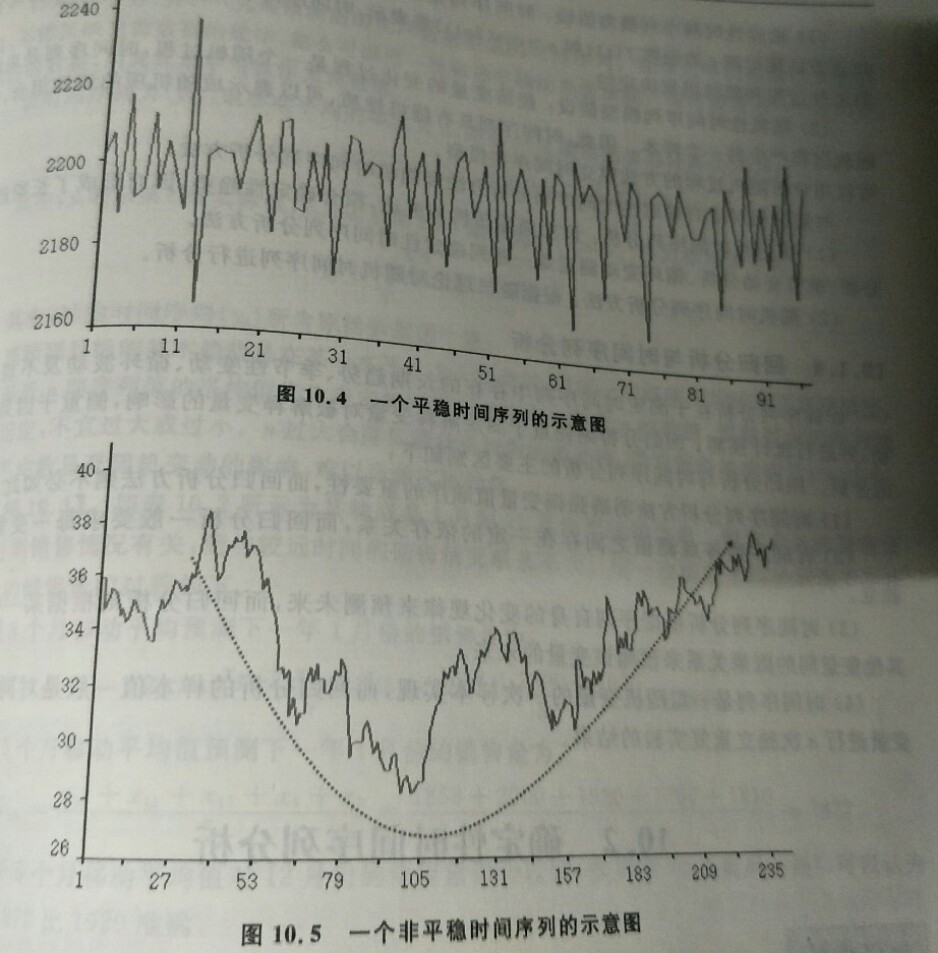
时间序列平稳性判断
利用散点图进行平稳性判断。直观判断散点图是否为一条围绕其平均值上下波动的曲线，如果是，则该时间序列是一个平稳时间序列。
利用自相关函数进行平稳性判断
一个时间序列为$（X_1,X_2,...,X_n）$，则$（X_t,X_{t-1},...,X_{t-k}）$之间的简单相关关系称为自相关，自相关函数$r_k$表示时间序列中相隔$k$期的观测值之间的相关程度：
$$ r_k = \frac{\sum_{t=1}^{n-k}(X_t-\overline X)(X_{t+k}-\overline X)}{\sum_{t=1}^{n}(X_t-\overline X)^2} $$
其中，$k$为滞后期，$\overline X$为样本均值。$r_k$的取值范围为[-1,1]，$|r_k|$越接近1，自相关程度越高，如果$r_k$迅速下降且趋向0，则认为该时间序列是一个平稳时间序列，否则认为它是一个非平稳时间序列。
时间序列建摸的两种基本假设
确定性时间序列模型假设：时间序列是由一个确定性过程产生的，这个确定性过程往往可以用时间t的函数$f(t)$（如$y=cos(2πt)$）来表示，时间序列中的每一个观测值是由这个确定性过程和随机因素决定的。
随机性时间序列模型假设：经济变量的变化过程是一个随机过程，时间序列是由该随机过程产生的一个样本。因此，时间序列具有随机性质，可以表示成随机项的线性组合，即可以用分析随机过程的方法建立时间序列模型。
确定性时间序列分析
移动平均模型
1.一次移动平均法
已知序列$y_1$、$y_2$、…、$y_n$是预测前的实际数据组成的时间序列。如果过早的数据已失去意义，不能反映当前数据的规律，那么可以用一次移动平均法来作预测。即保留最近一个时间区间内的数据，用其算术平均数作为预测值。
设时间序列为{$y_t$}，取移动平均的项数为n，则第t+1期预测值的计算公式为：
$$ \hat y_{t+1} = \frac{y_t+y_{t-1}+...+y_{t-n+1}}{n}=\frac{1}{n}\sum_{j=1}^{n}y_{t-n+j} $$
2.加权一次移动平均预测法
前面介绍的简单一次移动平均预测法，是把参与平均的数据在预测中所起的作用同等看待，但实际中参与平均的各期数据所起的作用往往是不同的。为此，需要采用加权移动平均法进行预测，加权一次移动平均预测法是其中比较简单的一种。其计算公式如下：
$$ \hat y_{t+1} = \frac{W_1y_t+W_2y_{t-1}+...+W_ny_{t-n+1}}{W_1+W_2+...+W_n} $$
指数平滑模型
1.一次指数平滑法
该方法利用前一时期的数据进行预测的方法。它适用于变化比较平稳，增长或下降趋势不明显的时间序列数据的下一期的预测。其模型是：
$$ \hat y_t = ky_{t-1}+(1-k)\hat y_{t-1} $$
2.二次指数平滑法
该方法是对一次指数平滑值再作一次指数平滑来进行预测的一种方法，但第t+1期预测值并非第t期的二次指数平滑值，而是采用下列计算公式进行预测：
$$ \begin{cases} S_t^{(1)}=ky_t+ (1-k)S_{t-1}^{(1)} \\ S_t^{(2)}=kS_t^{(1)}+ (1-k)S_{t-1}^{(2)} \\ \hat y_{t+T}=a_t+b_tT \\ \end{cases} $$
例题
